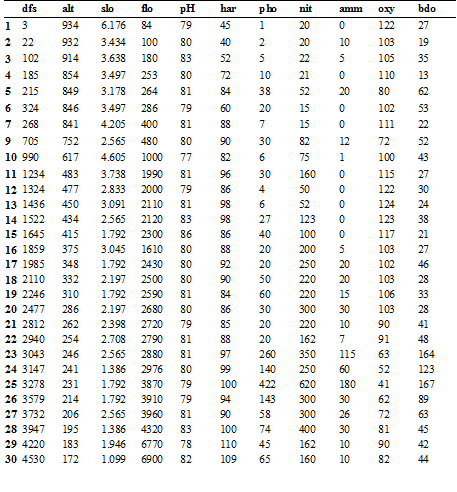
Ukázku výpočtu koinerční analýzy si představíme na datovém souboru, který obsahuje data pro 30 lokalit popsaných fyzickogeografickými a chemickými proměnnými (Tabulka 1). Pomocí CoIA budeme sledovat, zda geografické parametry souvisejí s parametry chemickými. Analýzu provedeme ve statistickém softwaru R doplněném o balík ade4 za použití funkce coinertia(). Nejdříve je potřeba provést analýzu hlavních komponent na každé sadě proměnných zvlášť, abychom získali dva ordinační prostory, které budeme následně srovnávat. Analýzu hlavních komponent provedeme na standardizovaných datech.

Tabulka 1: Datový soubor obsahující informace o 30 lokalitách, jež jsou popsány fyzickogeografickými a chemickými parametry

Fyzickogeografické parametry: dfs – vzdálenost od pramene (km * 10), alt – nadmořská výška (m), slo (ln(x+1) kde x je sklon (per mil * 100), flo – minimální průměrný průtok (m3/s *100)

Chemické parametry: pH (*10), har – celková tvrdost vody (mg/l of Ca), pho - fosfáty (mg/l*100), nit - nitráty (mg/l * 100), amm - ammoniak (mg/l * 100), oxy – rozpuštěný kyslík (mg/l * 10), bdo – biologická spotřeba kyslíku (mg/l * 10)

Následně provedeme koinerční analýzu a pomocí permutačního testu zjistíme statistickou významnost společné struktury.
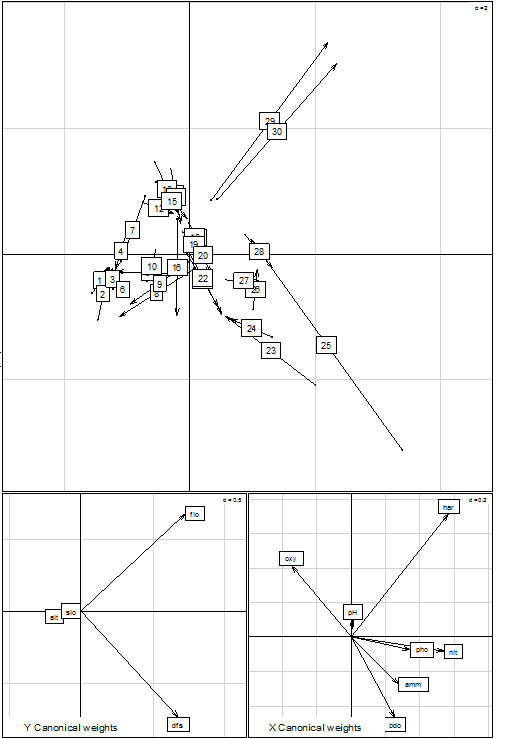
Výsledek CoIA je zobrazen na Obr. 1. Numerický výstup z CoIA je následující:

Eigenvalues decomposition:
eig covar sdX sdY corr
1 5070207.891 2251.71221 1.8690931 1395.90026 0.8630333
2 1839.624 42.89084 0.7600198 88.80363 0.6354903

Inertia & coinertia X (dudi.chem):
inertia max ratio
1 3.493509 3.914385 0.8924796
12 4.071139 5.219710 0.7799550

Inertia & coinertia Y (dudi.topo):
inertia max ratio
1 1948538 1948538 0.9999997
12 1956424 1956424 1.0000000

RV:
0.61144

V první části výsledků najdeme rozklad matice koinercie na vlastní čísla a vlastní vektory (eig – vlastní čísla, covar – kovariance, sdX a sdY– směrodatné odchylky) a korelace (corr) pro dvě sady skór pro lokality na koinerčních osách. Korelace je počítána jako .

Další blok výsledků porovnává inercii (kumulativně) projekce dat X a Y promítnuté v CoIA s maximem inercie získané z os z oddělených ordinací (max). Toto také udává podíl hodnot míry shody mezi dvěma projekcemi. Na závěr je uvedena hodnota RV koeficientu, což je vícerozměrné zobecnění Pearsonova korelačního koeficientu.

Tyto výsledky ukazují, že první vlastní číslo, které reprezentuje 99,0% celkové variance, je mnohem větší než druhé. Nejvíce společné struktury pro obě datové matice nese právě první osa. Horní graf (normované skóre objektů) ukazuje pozici lokalit na koinerčních osách za použití „chemických“ (počátky šipek) a „fyziografických“ (šipky) koinerčních vah. Krátké šipky ukazují na lepší shodu mezi dvěma projekcemi. Pár grafů dole ukazuje příspěvek dvou sad proměnných ke kanonickému prostoru. Vektory vykreslené stejným směrem jsou korelovány, delší vektory přispívají více k dané struktuře. Parametr „har“ (tvrdost vody) pozitivně koreluje s „flo“ (minimální průměrný průtok), parametr „oxy“ (rozpuštěný kyslík) negativně koreluje s „dfs“ (vzdálenost od pramene). Statistická významnost permutačního testu je 0,002, lze tedy konstatovat, že tyto dva soubory spolu souvisejí více, než by mohly spolu souviset dva náhodné datové soubory.

Obr.1: Grafický výstup z koinerční analýzy pro chemické a fyzickogeografické parametry. X představuje chemické parametry a Y fyzickogeografické (více viz text).

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity