Metriky pro určení vzdálenosti mezi dvěma množinami vektorů používající jejich pravděpodobnostní charakteristiky

Skupiny objektů či subjektů (tzn. množiny vektorů se společnými charakteristikami) nemusí být definovány jen výčtem vektorů, nýbrž vymezením obecnějších vlastností, jak je zmiňováno v kapitole o klasifikaci – tedy například definicí hranic oddělujících část vektorového prostoru, která náleží dané klasifikační třídě, diskriminační funkcí, pravděpodobnostními charakteristikami výskytu vektorů v dané třídě, atd. Jestliže jsme v předchozí kapitole využívali znalosti vlastností dané množiny, které byly určeny polohou jednotlivých konkrétních vektorů patřících do té které množiny, dále popíšeme způsoby stanovení vzdálenosti mezi množinami, které používají pravděpodobnostní charakteristiky rozložení vektorů v dané množině.

Pokud si na metriky klademe určité požadavky, i metriky pro stanovení vzdálenosti dvou množin, pro něž využíváme rozložení pravděpodobnosti výskytu vektorů, by měly vyhovovat standardním požadavkům. Tyto metriky splňují následující vlastnosti (protože jejich výpočet je založen na poněkud jiném přístupu a protože i dále uvedené vlastnosti nesplňují vždy vše, co od metrik očekáváme, bývá zvykem je značit jiným písmenem, zpravidla J):

1.  J = 0, pokud jsou hustoty pravděpodobnosti obou množin identické, tj. když

2.  ;

3.  J nabývá maxima, pokud jsou obě množiny disjunktní, tj. když

(Jak vidíme, není mezi vlastnostmi pravděpodobnostních metrik uvedena trojúhelníková nerovnost, jejíž splnění by se zajišťovalo vskutku jen velmi obtížně.)

Ilustrace jednotlivých vlastností pravděpodobnostních metrik je uvedena na Obr. 10:

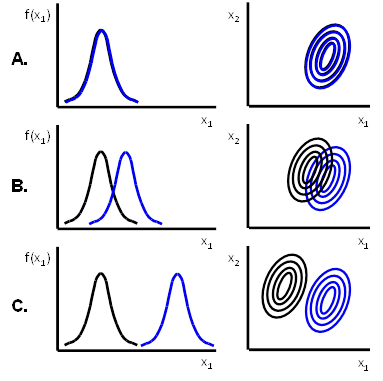
Základní myšlenkou, na které jsou pravděpodobnostní metriky založeny, je podobně, jak je popsáno pro Bayesovský klasifikátor, využití pravděpodobnosti způsobené chyby. Čím více se hustoty pravděpodobnosti výskytu vektorů x v jednotlivých množinách překrývají, tím je větší pravděpodobnost chyby.

Pokusme se nyní tuto myšlenku zformalizovat. Pravděpodobnost chybného zařazení je rovna

Tento vztah je možné odvodit ze vztahů popsaných v kapitole o kritériu minimální střední ztráty u Bayesova klasifikátoru .

Pro dichotomický případ (R = 2) je celková pravděpodobnost chybného rozhodnutí určena vztahem

což lze podle Bayesova vzorce upravit i do tvaru

Integrál ve vztahu (14) nazýváme Kolmogorovova variační vzdálenost a jeho hodnota přímo souvisí s pravděpodobností chybného rozhodnutí. Ostatní dále uvedené pravděpodobnostní míry vzdálenosti, odvozené z obecné formule

už tuto přímou souvislost nemají, ale mohou být použity k určení mezí odhadu chyby.

Jednou z hlavních nevýhod pravděpodobnostních metrik je potřeba odhadnout průběh hustot pravděpodobnosti a poté je integrovat, což může způsobit problémy, které znemožní použití tohoto přístupu v mnoha různých aplikacích. Situace se výrazně zjednoduší, pokud lze předpokládat určitý charakter rozložení pravděpodobnosti použít analytický popis pravděpodobnostních charakteristik. V tom případě je možné provést mnohé výpočty analyticky. Praktické úlohy ale často na analytický popis potřebných pravděpodobnostních charakteristik nevedou, je potřeba využít empirický (neparametrický) popis např. histogramem. Za takových podmínek nezbývá, než se s výpočty vypořádat numericky.

Mezi nejpoužívanější míry pravděpodobnostní vzdálenosti dvou množin patří

Chernoffova metrika

Bhattacharyyova metrika

(Jak lze snadno rozpoznat, Bhattacharyyova metrika je speciální případ Chernoffovy metriky pro s = 0,5).

Divergence

Patrickova -Fisherova metrika

Alternativou mohou být jejich zprůměrněné verze, které zahrnují i apriorní pravděpodobnost jednotlivých množin:

zprůměrněná Chernoffova metrika

zprůměrněná Bhattacharyyova metrika

zprůměrněná divergence

zprůměrněná Patrickova -Fisherova metrika

Pro R množin byl odvozen vztah pro Bayesovu metriku

Hodnoty vzdálenosti určené podle tohoto předpisu se pohybují v intervalu . Jednotkové hodnoty nabývá v případě, že aposteriorní pravděpodobnost  jedné množiny je rovna jedné, zatímco pro zbývající množiny jsou jejich aposteriorní pravděpodobnosti nulové. Nejmenší hodnoty, které Bayesova vzdálenost nabývá, je 1/R. To v případě, že jsou všechny aposteriorní pravděpodobnosti stejné. Když , pak se hodnota vzdálenosti limitně blíží k nule.

Uvedené vztahy se liší zejména pracností výpočtu a vazbou k hodnotám pravděpodobnosti chyby. Tato vazba je vyjádřena hodnotami dolního D(x) a horního H(x) odhadu pravděpodobnosti chyby, z nichž především horní odhad má praktický význam.

Pro některé z uvedených pravděpodobnostních měr jsou hodnoty horního odhadu

V případě, že známe dichotomické pravděpodobnostní míry a je třeba řešit problém klasifikace do více tříd, lze definovat metriku podle vztahu

V tom případě ale neplatí těsný vztah k hodnotě pravděpodobnosti chyby, jako ve výše uvedených vztazích.