
Příklad 4
Bylo provedeno měření výšky (v cm) a váhy
(v kg) u pěti dětí. Naměřené hodnoty byly zaznamenány do matice
:
U tohoto datového souboru proveďte analýzu hlavních komponent.
Řešení:
U analýzy hlavních komponent potřebujeme nejprve spočítat kovarianční matici . Pro výpočet kovarianční matice potřebujeme znát průměrnou výšku a váhu u
dětí:
Jednotlivé prvky kovarianční matice poté spočítáme následujícím způsobem:
Rozptyl výšky:
Rozptyl váhy:
Kovariance výšky a váhy:
Kovarianční matice je tedy:
.
Nyní spočítáme vlastní čísla a vlastní vektory kovarianční matice – tzn., spočítáme následující determinant:
Vypočteme charakteristický polynom:
A jeho kořeny, které odpovídají vlastním číslům:
Následně spočítáme vlastní vektor odpovídající prvnímu vlastnímu číslu
:
;
; např. pro
pak dostáváme:
, který je po normalizaci roven
. Kontrola, že vektor má jednotkovou délku:
.
Spočítáme vlastní vektor odpovídající druhému vlastnímu číslu
:
;
; např. pro
pak dostáváme:
, který je po normalizaci roven
. Kontrola, že vektor má jednotkovou délku:
.
Vlastní vektory můžeme uspořádat do matice , přičemž pořadí vlastních vektorů odpovídá pořadí vlastních čísel seřazených od největšího k nejmenšímu.
Nyní vyjádříme hlavní komponenty odpovídající vlastním číslům seřazeným od největšího k nejmenšímu – hlavní komponenty jsou lineární kombinace původních proměnných, přičemž koeficienty jsou souřadnice příslušného vlastního vektoru:
- hlavní komponenta:
(pro
)
- hlavní komponenta:
(pro
)
Výpočet procent vyčerpané variability:
- hlavní komponenta vyčerpává:
(tzn., 92,93% variability v datech)
- hlavní komponenta vyčerpává:
(tzn., 7,07% variability v datech)
Vyčerpanou variabilitu můžeme znázornit i pomocí sutinového grafu:

Dále spočítáme korelace hlavních komponent s původními proměnnými:
První hlavní je vysoce korelována s váhou a středně korelována s výškou. Druhá hlavní komponenta je středně záporně korelována s výškou.
Na závěr vypočítáme nové souřadnice původních bodů po transformaci pomocí obou hlavních komponent spočítaných pomocí PCA:
Souřadnice subjektů můžeme přímo získat i z hlavních komponent – např. pro první subjekt:
Původní data i data po transformaci pomocí PCA si znázorníme:
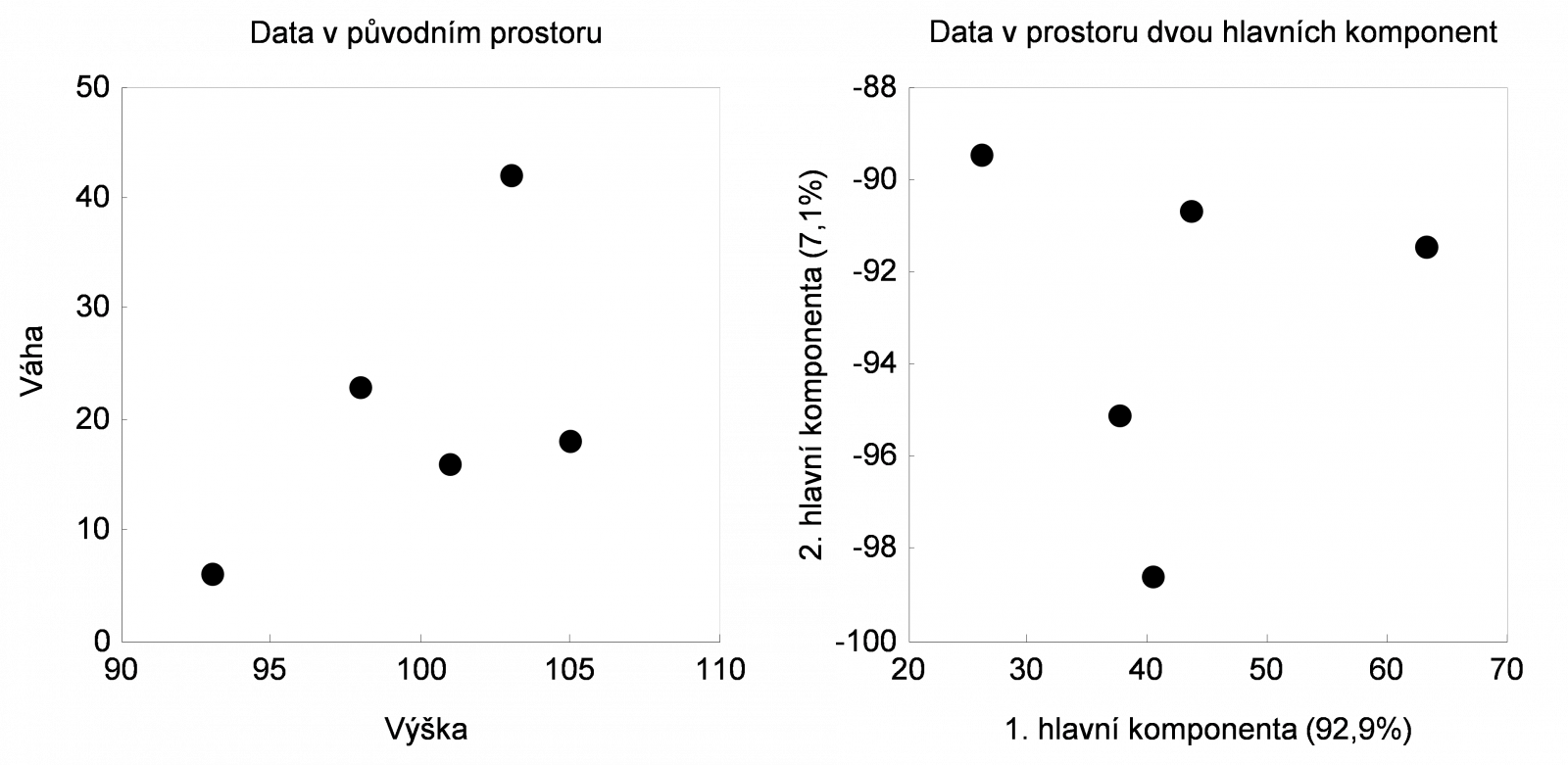
Pokud bychom k transformaci použili pouze první vlastní vektor, získáváme data v prostoru první hlavní komponenty:





