Slovník | Vyhledávání | Mapa webu
 
Analýza a hodnocení biologických datVícerozměrné metody pro analýzu a klasifikaci dat Podobnosti a vzdálenosti ve vícerozměrném prostoru Praktické příklady
Logo Matematická biologie

Praktické příklady

Příklad 1

Zjistěte, zda má subjekt  kratší vzdálenost (tzn. je podobnější) k subjektu  či k subjektu  pomocí Euklidovy, Hammingovy (manhattanské), Čebyševovy a Canberrské metriky.

 

Řešení:

  1. Euklidova metrika
 

 Vzdálenost je stejná.

  1. Hammingova (manhattanská) metrika

Vzdálenost je stejná.

  1. Čebyševova metrika

Vzdálenost je stejná.

  1. Canberrská metrika

Subjekt  má kratší vzdálenost od subjektu  než od subjektu , tzn. subjekt  je podobnější subjektu  než subjektu .

 

Příklad 2

Určete hodnoty Jaccardova, Russel-Raova, Sokal-Michenerova, Dicova, Rogers-Tanimotova a Hamanova koeficientu pro dvě lokality podle výskytu šesti druhů drobných zemních savců uvedených v tabulce 1.

Tabulka 1. Výskyt šesti druhů drobných zemních savců (DZS) na dvou lokalitách v roce 2005. Chionomys nivalis (Ch.n.), Clethrionomys glareolus (C.g.), Microtus tatricus (M.t.), Microtus agrestis (M.agr.), Apodemus flavicollis (A.f.), Sorex araneus (S.a.). (Nepublikovaná data I. Čornaninová).

Řešení:

V posledním řádku tabulky uvedeme označení stavu jednotlivých souřadnic obou vektorů.

Z toho vyplývá, že A = 2, B = 2, C = 1, D = 1, což můžeme zapsat do kontingenční tabulky:

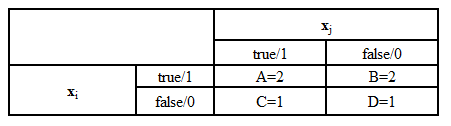
Jaccardův-Tanimotův koeficient pro naše dvě lokality pak bude:

.

Russelův-Raoův koeficient:

.

Sokalův-Michenerův koeficient:

.

Dicův koeficient:

.

Rogersův-Tanimotův koeficient:

.

Hamanův koeficient:

.

 
vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity