Algoritmus ohraničeného větvení

Umožňuje stanovit optimální množinu proměnných za předpokladu, že kriteriální funkce pro selekci proměnných je monotónní. Označíme-li množinu proměnných, pak monotónnost kriteriální funkce znamená, že pro množiny

splňuje selekční kriteriální funkce vztah

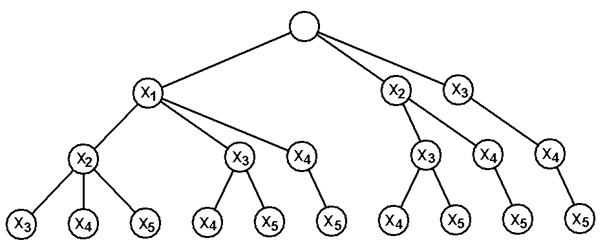
Pro popis algoritmu uvažme případ selekce dvou proměnných z původních pěti. Všechny možné alternativy vyloučení tří proměnných z výchozí množiny ukazuje graf na Obr.3. Každý uzel v grafu vyjadřuje eliminaci jedné označené proměnné.

Předpokládejme, že vyhodnocujeme hodnotu zvolené kriteriální funkce v každém uzlu stromu, přičemž postupujeme shora dolů a zleva doprava, a srovnáváme ji s dosud nejlepší (největší) dosaženou hodnotou, kterou označíme . Pokud je okamžitá hodnota kriteriální funkce větší než , je stále šance, že optimální řešení bude nalezeno na právě analyzované větvi grafu, a proto bude hledání pokračovat po nejlevější dosud neanalyzované větvi. Jestliže dosáhneme konce větve a odpovídající hodnota selekčního kritéria je větší než , pak tento uzel definuje novou optimální množinu proměnných a modifikujeme hodnotu . Naopak, jestliže je v některém uzlu grafu hodnota selekčního kritéria menší než , pak větve začínající v tomto uzlu nemá smysl dále prohledávat, protože díky monotónnosti kritéria budou jeho hodnoty v dalších uzlech již jenom menší.

Efektivnost prohledávání se ještě zvětší, jestliže se bude výběr odstraňované veličiny na dané úrovni stromu provádět podle změny hodnoty kriteriální funkce a bude se postupovat tím směrem, kde je změna kriteriální funkce nejmenší.

Příklad 5:

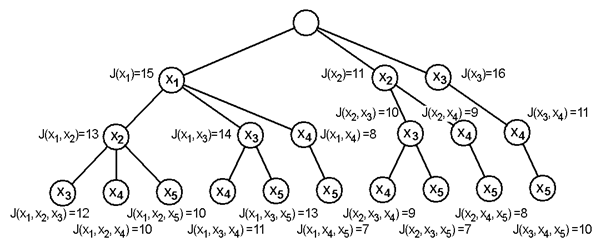
Jsou-li jednotlivé uzly algoritmu ohraničeného větvení pro selekci 2 z 5 ohodnoceny hodnotami kriteriální funkce podle Obr.4, určete cestu procházení grafu algoritmu, využije-li se základní formy algoritmu.

Řešení:

Postupujeme z kořenového uzlu přes uzly , do ,  = 12. Návratem přes uzel do uzlu , resp. (v obou případech je hodnota kriteriální funkce rovna 10, tj. menší než ). Návrat do uzlu a pak postup do uzlu . Hodnota kriteriální funkce je rovna 14, tj. je větší než , lze tedy pokračovat na nižší úroveň do uzlu , resp. . V tomto uzlu je hodnota kriteriální funkce větší než dosavadní hodnota , proto dojde k její modifikaci na = 13. Návrat přes uzel do uzlu . Zde již je hodnota kriteriální funkce menší než současná hodnota , není proto třeba pokračovat větví dále. Následuje postup přes kořenový uzel do větve začínající uzlem . Kriteriální funkce je zde menší než , proto není potřeba pokračovat v prohlížení větve do nižších úrovní. Po návratu přes kořenový uzel pokračujeme do větve začínající uzlem . Protože kriteriální funkce nabývá větší hodnoty než , lze pokračovat dále. V následujícím uzlu je však hodnota kriteriální funkce menší než , proto prohledávání grafu končí. Optimální je tedy odstranění proměnných , a , a tudíž výsledkem je selekce proměnných a .