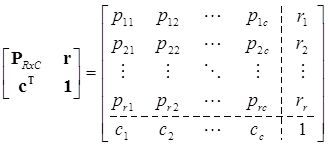Základní pojmy u korespondenční analýzy
Mějme matici typu
x
odpovídající kontingenční tabulce dvou kategoriálních proměnných, přičemž
a
, kde
a
je počet kategorií u první respektive druhé proměnné, celkový počet
a okrajové četnosti
a
.
Matice se nazývá korespondenční matice a vypočteme ji podílem matice
a celkového počtu pozorování
. Jednotlivé prvky matice
získáme jak
|
|
(1) |
Řádkové zátěže vypočteme podílem okrajových četností
celkovým počtem
|
|
(2) |
a -členný vektor řádkových zátěží označíme
.
Sloupcové zátěže vypočteme podílem okrajových četností
celkovým počtem
|
|
(3) |
a -členný vektor sloupcových zátěží pak označíme
.
Řádkové profily odpovídají podílu četností
a okrajových četností
, jde tedy o podmíněné relativní četnosti
|
|
(4) |
Matici řádkových profilů definujeme jako
|
|
(5) |
kde je diagonální matice s prvky vektoru
na diagonále.
Sloupcové profily vypočteme jako podíl
a
|
|
(6) |
Matici sloupcových profilů vypočteme jako
|
|
(7) |
kde je diagonální matice s prvky vektoru
na diagonále.
Korespondenční matici můžeme vyjádřit následovně:
|
|
(8) |
Zopakujme, že korespondenční analýza sleduje vztahy mezi řádky a sloupci kontingenční tabulky. V případě nezávislosti znaků v kontingenční tabulce platí shoda všech řádkových profilů a jejich rovnost s vektorem sloupcových zátěží. Podobně platí shoda všech sloupcových profilů a jejich rovnost s vektorem řádkových zátěží. Z uvedeného plynou další důležité vztahy v korespondenční tabulce. Vektor řádkových zátěží je ekvivalentní váženému součtu sloupcových profilů , s vahami okrajových relativních četností
.
|
|
(9) |
Podobně vektor sloupcových zátěží je roven váženému součtu vektorů řádkových profilů s vahami
.
|
|
(10) |