
Metoda nejbližšího souseda
Je-li D libovolná metrika vzdálenosti dvou vektorů a a
jsou libovolné množiny vektorů {xi}, i = 1, …, K, potom metoda nejbližšího souseda definuje vzdálenost mezi množinami
a
|
|
(60)
|
tedy vzdálenost mezi množinami je dána jako minimální vzdálenost mezi všemi možnými zástupci shluků (Obr. 4). To znamená, že v daných množinách nás zajímají pouze ty dva objekty, které jsou k sobě nejblíže.
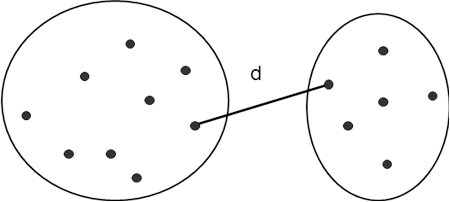
Při použití tohoto způsobu výpočtu vzdálenosti se mohou vyskytovat v jedné množině často i poměrně vzdálené vektory, pokud se mezi nimi vyskytují vektory další. To znamená, že metoda nejbližšího souseda může vytvářet klasifikační třídy protáhlého tvaru.
Příklad 7.1
Předpokládejme, že jsou zadány tři vzorové vektory x1 = (0, 0), x2 = (8, 8) a x’2 = (10, 10), které představují dvě klasifikační třídy. Rozhodněte, do které klasifikační třídy se zařadí vektor x = (5, 4). Pro výpočet vzdálenosti mezi dvěma vektory použijte Hammingovu metriku, pro výpočet vzdálenosti od obou klasifikačních tříd použijte metodu nejbližšího souseda.
Řešení:
Hammingova metrika je definována vztahem
Podle něj jsou vzdálenosti d(x,x1) = 5 + 4 = 9; d(x,x2) = 3 + 4 = 7 a d(x,x’2) = 5 + 6 = 11.
První třída obsahuje pouze jeden vektor, ten tím pádem zároveň představuje nejbližšího souseda ze třídy první. Druhá třída obsahuje dva vektory, z nichž bližší vektoru x je vektor x2 (to je nejbližší soused ze třídy druhé). Protože klasifikace podle minimální vzdálenosti zařazuje vektor do té množiny, jejíž nejbližší soused má od vektoru nejmenší vzdálenost, zařadíme vektor x do druhé třídy.
Předpokládejme, že na vstup shlukovacího algoritmu přicházejí objekty, které jsou dány vektory x1 = (0, 0), x2 = (10, 10), x3 = (8, 8), x4 = (6, 7), x5 = (4, 3) a x6 = (3, 2) v uvedeném pořadí. Proveďte shlukování daných objektů, přičemž vzdálenost mezi dvěma vektory určete podle Hammingovy metriky. Rozhodnutí, zda vektory patří do téhož shluku, bude záviset na prahové hodnotě dmez = 7. Vzdálenost mezi vektorem a shlukem určete na základě metody nejbližšího souseda.
Řešení:
První vektor x1 = (0, 0) je považován za představitele prvního shluku. Druhý vektor x2 = (10, 10) má od vektoru x1 vzdálenost d(x1,x2) = 10 + 10 = 20. To je vzdálenost větší než zadané dmez. Budeme jej proto považovat za představitele druhého shluku.
Vzdálenosti vektoru x3 od obou shluků reprezentovaných vektory x1 a x2 jsou d(x3,x1) = 8 + 8 = 16 a d(x3,x2) = 2 + 2 = 4. Vzdálenost d(x3, x2) je menší z obou a současně je i menší než dmez, bude proto vektor x3 zařazen do druhého shluku.
Pro x4 jsou vzdálenosti d(x4,x1) = 6 + 7 = 13 dmez, d(x4,x2) = 4 + 3 = 7 a d(x4,x3) = 2 + 1 = 3. Nejbližší soused vektoru x4 z druhého shluku je proto vektor x3, vzdálenost d(x4,x3)
dmez, tedy x4 zařadíme rovněž do druhého shluku, který už v tomto okamžiku zahrnuje vektory C 2 = {x2, x3, x4}.
Ekvivalentně postupujeme i v případě vektoru x5. Pro vektor x6 je vzdálenost od prvního shluku daná d(x6,x1) = 3 + 2 = 5 dmez a nejbližší soused z druhého shluku je vektor x5, pro který je d(x6,x5) = 1 + 1 = 2
dmez. Obě vzdálenosti jsou menší než dmez, je ale d(x6,x1)
d(x6,x5), proto vektor x6 zařadíme opět do druhého shluku.
Po zpracování všech vektorů jsou vytvořeny dva shluky = {x1} a
= {x2, x3, x4, x5, x6}. Jak je zřejmé, shluk
vytváří velice protáhlou strukturu.
Příklad 7.3
Předpokládejme totéž zadání jako v příkladu 7.2, pouze zpracování vektorů x5 a x6 proběhne v opačném pořadí.
Skryté řešení:
Vzhledem v podstatě k témuž zadání jako v příkladu 7.2, bude řešení až po zpracování řetězců x5 a x6 stejné.
Pro dříve zpracovávaný vektor x6 je d(x6,x1) = 3 + 2 = 5 dmez a nejbližší soused z druhého shluku je v tomto případě x4, pro který platí d(x6,x4) = 3 + 5 = 8
dmez. Vektor x6 proto tentokrát zařadíme do prvního shluku.
Konečně, pro poslední vektor x5 je nejbližší soused z prvního shluku vektor x6, pro který je d(x5,x6) = 1 + 1 = 2 dmez a z druhého shluku je nejbližší soused opět vektor x4, pro který je d(x5,x4) = 2 + 4 = 6
dmez. Protože d(x5,x6)
d(x5,x4), je vektor x5 zařazen do prvního shluku.
Po zpracování všech vektorů jsou s tímto pořadím zpracování posledních dvou vektorů vytvořeny dva shluky = {x1, x5, x6} a
= {x2, x3, x4}.




