Vektorem a rozumíme uspořádanou n-tici prvků a_i, i = 1, …, n. Prvky vektoru jsou nejčastěji čísla, ale mohou jimi být libovolné matematické objekty. Vektor zpravidla zapisujeme ve tvaru a = (a₁, a₂, … a_n), používá se někdy také značení a(a₁, a₂, … a_n).

Vektorem může být n-tice prvků uspořádaná do řádku (tak, jak je zde uvedeno), nebo i do sloupce.

Složky vektoru mohou být považovány za souřadnice bodu v -rozměrném prostoru, který vektor reprezentuje. Pokud je prostor euklidovský (tj. určujeme v něm vzdálenost podle Euklidovy metriky), lze určit délku (modul) |a| vektoru a = (a₁, a₂, …, a_n) (vzdálenost jeho koncového bodu od počátku) pomocí vztahu vycházejícího ze zobecněné Pythagorovy věty

(1)

Obr.1: Zobrazení vektoru a = (4,3) v euklidovském prostoru

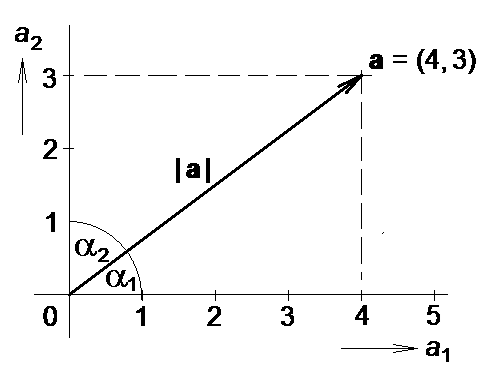
Příklad Vektory.1

Dvourozměrný vektor a = (a₁, a₂) = (4, 3) zobrazený na Obr. 1 má v euklidovském prostoru délku podle vztahu (1) rovnu

Úhly, které vektor svírá s osami souřadnic, se nazývají směrové úhly a jejich kosiny jsou označovány jako směrové kosiny daného vektoru. Označíme-li α₁, α₂, …, α_n směrové úhly vektoru a = (a₁, a₂, …, a_n) ≠ 0, pak pro jeho směrové kosiny platí

;	(2a) (2b)

Příklad Vektory.2

Ze vztahu (2a) odvoďte vztah (2b)

Skryté řešení:

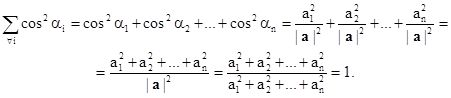
Příklad Vektory.3

Zdůvodněte, proč si klademe v definici směrového kosinu podmínku a = (a₁, a₂, …, a_n) 0, resp. |a| 0.

Skryté řešení:

U vektoru nulové délky (tj. v podstatě reprezentovaného pouhým bodem) nejsme schopni určit směrové úhly.

Vysvětlení pojmu Vektory.2

Ke každému nenulovému vektoru a existuje jednotkový (normalizovaný) vektor , který má jednotkovou délku (modul) a má s vektorem a stejný směr. Říkáme, že je s vektorem a souhlasně rovnoběžný. Pro jeho souřadnice platí

(3)

Ze srovnání vztahů (2a) a (3) je

(4)

Poznámka

Při řešení klasifikačních úloh je potřeba si uvědomit, že úplná informace, kterou nesly původní vektory, je normalizací redukována pouze na informaci směrovou (moduly vektorů jsou po normalizaci všechny stejné – jednotkové). To samozřejmě nemusí být na závadu, pokud je směrová informace z hlediska řešené úlohy ta podstatná. Ovšem minimálně je třeba mít možné důsledky normalizace na paměti dříve, než se provede.

Dva vektory a = (a₁, a₂, … a_n) a b = (b₁, b₂, … b_n) se sobě rovnají tehdy a jen tehdy, pokud se rovnají hodnoty všech jejich složek, tj. a₁= b₁, a₂= b₂, …, a_n = b_n.

Příklad Vektory.4

Pokuste se na základě této poučky zdůvodnit, že záleží na zachování pořadí jednotlivých složek vektoru.

Skryté řešení:

Máme-li srovnat dva vektory, je nezbytné srovnávat položky, které si významově odpovídají. Pokud bychom nerespektovali význam jednotlivých složek vektoru v daném pořadí, nebylo by možné vektory srovnávat.

Vysvětlení pojmu Vektory.3

Součtem dvou vektorů a = (a₁, a₂, … a_n) a b = (b₁, b₂, … b_n) je opět vektor c = a + b, jehož souřadnice jsou dány součtem dílčích souřadnic obou vstupních vektorů, tj. c = (a₁+b₁, a₂+b₂, … a_n+b_n).
Součinem vektoru a = (a₁, a₂, … a_n) s číslem k je opět vektor c = k.a, jehož složky jsou k-násobkem složek vektoru a, tj. c = (ka₁, ka₂, …, ka_n).

Z Vysvětlení pojmuVektory2.3 platí pro operace s vektory následující pravidla:

Obr.2: Součet vektorů

a + b = b + a (komutativní zákon);
a + (b + c) = (a + b) + c (asociativní zákon);
existuje tzv. nulový vektor 0 = (0, 0, …, 0), pro nějž je a + 0 = a;
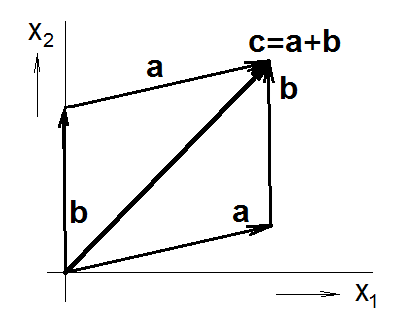
k vektorům a = (a₁, a₂, … a_n) a b = (b₁, b₂, … b_n) existuje vektor c = (a₁-b₁, a₂-b₂, … a_n-b_n), že platí a = b + c (Obr. 2 – z tohoto obrázku vyplývá i komutativnost sčítání dvou vektorů);
distributivní zákony: k.(a + b) = k.a + k.b , (k+m).a=k.a+ m.a;
c.(d.a) = (c.d).a
0.a = 0 a k.0 = 0, z čehož plyne, že rovnost k.a = 0 nastane pouze tehdy, pokud k = 0 nebo a = 0;
-(ka) = (-k).a = k.(-a).

Součin dvou vektorů má dvě podoby. U tzv. skalárního součinu, který je definován vztahem

(5)

je výsledkem skalár (číslo). Pro skalární součin platí i vztah

(6)

kde je úhel, který svírají vektory a a b.

Jsou-li oba vektory rovnoběžné, tj. , a proto = 1, pak = |a|.|b|. Jsou-li vektory a k sobě kolmé, tj. = 90° nebo jinak , a proto = 0, pak = 0. Toto tvrzení lze i otočit a říci, že nenulové vektory a a b jsou k sobě kolmé, právě když platí = 0.

Pro skalární součin vektorů a dále platí:

Obr.3 Pravidlo pravé ruky pro stanovení orientace vektorového součinu

a.b = b.a;
(a + b).c = a.c + b.c;
a.a = |a|².

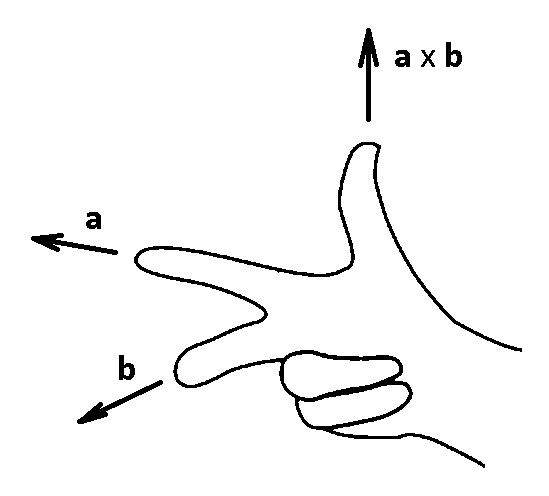
V případě tzv. vektorového součinu je výsledkem vektor kolmý k oběma zadaným vektorům (tj. platí w.a = 0 i w.b = 0, jeho délka je rovna obsahu rovnoběžníka určeného vektory a a b, tj.

|w| = |a|.|b|.sinα, kde α je opět úhel, který svírají vektory a . Orientace vektoru w je určena podle pravidla pravé ruky (Obr. 3).

Pro vektorový součin platí:

a × b = -(b × a) – tzn. pozor na pořadí, komutativní zákon pro vektorový součin neplatí;
k.a × b = k.(a × b);
a × (b + c) = a × b + a × c.

Vysvětlení pojmu Vektory.4:

Vektory a₁, a₂, …, a_m jsou lineárně závislé, pokud existují taková čísla c₁, …, c_m, z nichž alespoň jedno je různé od nuly, že platí

(7)

Příklad Vektory.5

Vektory a₁ = (4, 0, 2), a₂ = (2, 3, 2) a a₃ = (6, 0, 3) jsou lineárně závislé, protože pro c₁ = -3, c₂ = 0 a c₃ = 2 platí, že (-3).(4, 0, 2) + 0.(2, 3, 2) + 2.(6, 0, 3) = (0, 0, 0).

Příklad Vektory.6

Vektory e₁ = (1, 0, 0), e₂ = (0, 1, 0) a e₃ = (0, 0, 1) nejsou lineárně závislé, protože neexistují žádná čísla c₁, c₂, c₃, pro která by platilo c₁e₁ + c₂e₂ + c₃e₃= 0. Protože navíc platí, že e₁.e₂ = e₂.e₃ = e₁.e₃ = 0, můžeme konstatovat, že vektory e₁, e₂, e₃ jsou navzájem kolmé a tvoří tzv. ortogonální soustavu vektorů. Protože délka vektorů e₁, e₂ a e₃ je ve všech případech jednotková, je soustava vektorů e₁, e₂, e₃ i ortonormální.

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity