Srovnání úspěšnosti klasifikace dvou klasifikátorů

V praxi se stává často, že potřebujeme srovnat úspěšnost dvou klasifikátorů. Například, pokud vytvoříme novou klasifikační metodu či modifikaci stávající klasifikační metody a chceme ukázat, že funguje lépe než stávající metoda. Znalost metod pro srovnání úspěšnosti klasifikace jednotlivých klasifikátorů je tedy nezbytná.

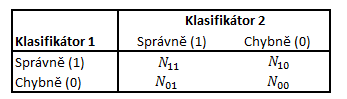
Srovnání úspěšnosti klasifikace dvou klasifikátorů můžeme provést pomocí McNemarova testu či dvouvýběrového binomického testu. V obou případech se vychází z tabulky, která srovnává počty správně a chybně klasifikovaných subjektů pomocí obou metod (Tab. 2), přičemž , kde  je počet subjektů správně klasifikovaný oběma klasifikátory,  je počet subjektů správně klasifikovaný prvním klasifikátorem a chybně klasifikovaný druhým klasifikátorem,  je počet subjektů správně klasifikovaný druhým klasifikátorem a chybně klasifikovaný prvním klasifikátorem,  je počet subjektů chybně klasifikovaný oběma klasifikátory a  je celkový počet testovacích subjektů.

McNemarův test pak vypočítáme jako:

(8)

kde hodnota -1 v čitateli je korekce na spojitost. Pokud , zamítáme nulovou hypotézu o shodnosti celkové správnosti klasifikace pomocí dvou klasifikátorů.

Dvouvýběrový binomický test můžeme spočítat jako:

(9)

kde  , a . Pokud , zamítáme nulovou hypotézu o shodnosti podílu správně klasifikovaných subjektů dvou klasifikátorů. Dvouvýběrový binomický test však předpokládá nezávislost (tzn., že každý klasifikátor byl testován na jiném testovacím souboru), což není splněno, proto je doporučováno používat raději McNemarův test.

Příklad 4

Srovnejte úspěšnost klasifikace metody nejbližšího souseda (1-NN) z Příkladů 2 a 3 s klasifikací stejného testovacího souboru 100 subjektů pomocí metody podpůrných vektorů (SVM). Výsledky klasifikace oběma klasifikátory jsou uvedeny v tabulce:

Řešení

Pro snadnější výpočet si k tabulce dopočítáme součty v řádcích a sloupcích:

McNemarův test pak vypočteme jako  což je větší než 3,841, tudíž zamítáme nulovou hypotézu o shodnosti úspěšnosti klasifikace pomocí daných dvou klasifikátorů.

Dvouvýběrový binomický test spočítáme při znalosti  ,   a  jako   což v absolutní hodnotě není větší než 1,96, tudíž nezamítáme nulovou hypotézu o shodnosti úspěšnosti klasifikace pomocí daných dvou klasifikátorů.

Klasifikace pomocí metody nejbližšího souseda s celkovou správností 78% má tedy podle McNemarova testu statisticky významně horší úspěšnost než metoda podpůrných vektorů s celkovou správností 85%, zatímco podle dvouvýběrového binomického testu není statisticky významný rozdíl mezi oběma klasifikačními metodami. Protože však víme, že je doporučováno použití McNemarova testu namísto dvouvýběrového binomického testu, přikloníme se k tomu, že metoda podpůrných vektorů je pro náš datový soubor statisticky významně úspěšnější než metoda nejbližšího souseda.