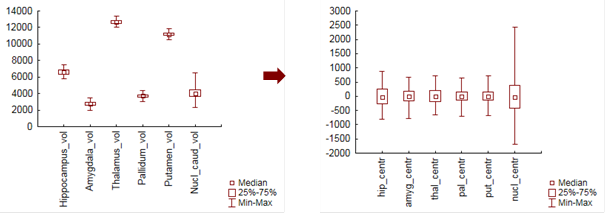
Centrování dat

Další úpravou dat, která se před použitím vícerozměrných analýz občas používá, je centrování dat. Při centrování je od původní hodnoty odečítán průměr proměnné, tj. od prvků sloupce se odečte jejich sloupcový průměr:

(31)

Získáme tedy nové proměnné, jejichž průměry jsou rovny nule (Obr. 8). Centrování se používá například u vícenásobné lineární regrese, kdy nemusíme uvažovat intercept, pokud jsou proměnné vstupující do modelu centrované.