Výhody a nevýhody NMDS

Nevýhodou NMDS je iterativní proces, který nemůže garantovat dosažení globálního, ale pouze lokálního optima při výpočtu souřadnic objektů. Druhou nevýhodou je nutnost specifikovat počet dimenzí předem. NMDS je citlivé vůči nesprávnému stanovení dimenzionality. Výsledná řešení jsou silně závislá na počtu dimenzí. První dva rozměry třírozměrného řešení NMDS nejsou stejné jako dvourozměrné řešení. Pro správné nastavení dimenzionality se doporučuje vykreslit hodnoty STRESSu pro různé počty rozměrů. Náhlé zploštění křivky v grafu ukazuje počet rozměrů, kdy už další řešení s vyšším počtem rozměrů není nutné.

Výhodou NMDS je jeho robustnost vůči odlehlým hodnotám a použitelnost i v případě nekompletních dat. Nemetrické vícerozměrné škálování může sloužit pro přípravu podkladů pro shlukovací metodu k-průměrů, pokud není možné na data použít výpočet vzdálenosti pomocí Euklidovy metriky.
Metoda NMDS je nejenom praktická metoda, ale v současnosti do jisté míry i módní záležitost.

Příklad 1
Nemetrické mnohorozměrné škálování představíme na příkladu korýšů šesti lokalit sledovaných ve třech časových obdobích. Vstupní matici tvořilo 63 taxonů korýšů vyskytujících se na šesti lokalitách v záplavové oblasti Dunaje ve třech obdobích (1: 1991–1992 před přehrazením Dunaje, 2: 1993–1997 prvních 5 let po přehrazení, 3: 1999–2004 dalších 6 let po přehrazení). Sledovanými lokalitami byly: D: Dobrohošť, G: Gabčíkovo, B: Bodíky, I: Istragov, K: Kráľovská lúka, S: Sporná sihoť. Početnost jednotlivých taxonů korýšů byla kvantifikována na desetistupňové škále.

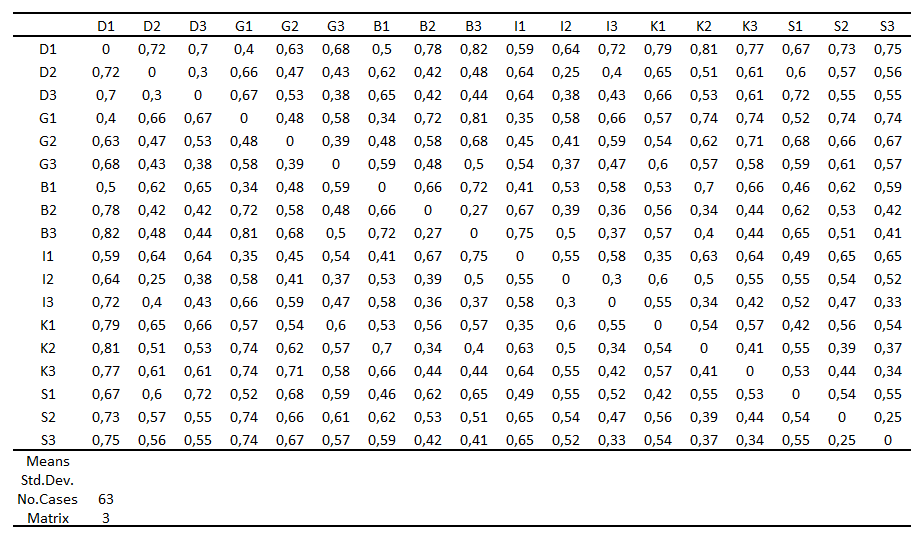
Z původní datové matice byla spočítaná matice Bray-Curtisovy vzdálenosti mezi všemi objekty (Tabulka 12). Tato vzdálenost (resp. nepodobnost) bývá velice často používána v biologii a ekologii ke kvantifikaci nepodobnosti společenstev lokalit. Pro výpočet Bray-Curtisovy vzdálenosti mezi objekty byl použit software Syn-Tax. Matice vzdáleností byla pak vstupem pro NMDS v softwaru Statistica. V tomto softwaru musí matice vzdáleností splňovat předepsaný formát. První část tvoří čtvercová matice vzdáleností (v našem případě prvních 19 řádků), druhou část tvoří čtyři řádky s předepsanými názvy: Means, Std.Dev. (tyto řádky nemusí být vyplněny, názvy řádků jsou ovšem nutné), No.Cases (počet proměnných použitých k výpočtu vzdáleností, v našem případě 63), Matrix (označení typu asociační matice, v našem případě hodnota 3 označuje matici vzdáleností).

Tabulka 12: Bray-Curtisovy vzdálenosti šesti lokalit ve třech časových obdobích spočítané na základě 63 taxonů korýšů (legenda v textu).

Kromě stanovení míry nepodobnosti bylo před samotnou analýzou potřeba nastavit také počet rozměrů, tj. dimenzionalitu řešení. Zvolili jsme počet rozměrů R = 2, jelikož jsme předpokládali dva faktory, které by mohly ovlivňovat společenství korýšů ve sledovaných objektech a tím definovat jejich vzájemné vztahy. Těmito předpokládanými faktory byl čas (období výzkumu) a prostor (geografická odlišnost jednotlivých odběrových lokalit).

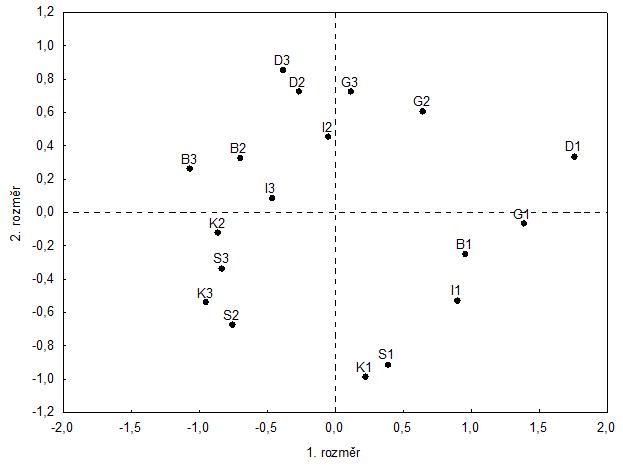Obr. 6: Konfigurace bodů jako výsledek nemetrického mnohorozměrného škálování šesti lokalit ve třech časových obdobích podle 63 taxonů korýšů (příklad z tabulky 12; legenda v textu).

Na výsledné konfiguraci ve dvourozměrném prostoru (Obr. 6) je vidět vztahy mezi jednotlivými odběrovými lokalitami a časovými obdobími. Při interpretaci se můžeme zaměřit na souřadné osy nebo na skupiny objektů. V našem příkladu se jako nejvhodnější jeví využití obou možností.

Podél prvního rozměru se téměř dokonale oddělily lokality sledované v prvním období výzkumu. V pravé polovině konfigurace bodů jsou umístěny všechny lokality před přehrazením Dunaje a dále lokalita Gabčíkovo z obou dalších období výzkumu. Z grafu je ovšem zjevné, že všechny lokality v prvním období výzkumu tvoří jednu skupinu, dobře oddělenou od ostatních objektů. Podél druhé osy můžeme vidět postupně seřazené lokality Sporná sihoť, Kráľovská lúka, Istragov, Bodíky, Gabčíkovo, Dobrohošť a když se díváme pouze na lokality sledované ve druhém a třetím období, nejsou zjevné žádné rozdíly mezi druhým a třetím obdobím výzkumu. Můžeme tedy konstatovat, že první období před přehrazením Dunaje bylo z hlediska společenstev korýšů zcela odlišné od dalších dvou časových období. V dalších dvou sledovaných časových obdobích je zřejmá spíše prostorová podobnost společenstev korýšů než časová.

Výsledek NMDS je podobný výsledkům hierarchického aglomerativního shlukování i shlukování metodou TWINSPAN (Shluková hierarchická analýza  ), při použití NMDS se ovšem výsledek zdá být nejlépe interpretovatelný.

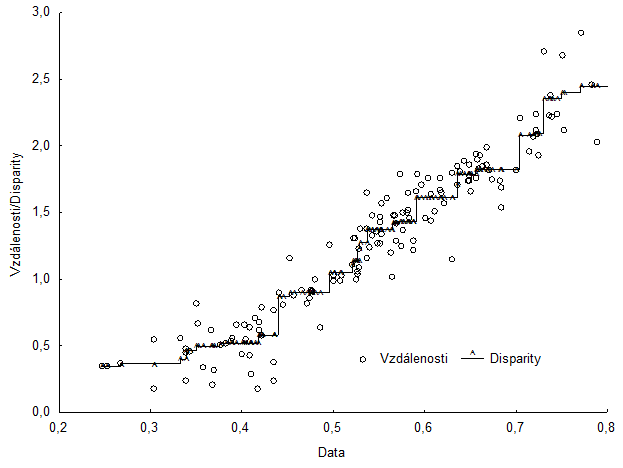Obr. 7: Ukázka Shepardova diagramu z NMDS. Na ose x jsou zobrazeny původní nepodobnosti, na ose y vzdálenosti v konfiguraci a disparity (Tabulka 12, Obr. 6).

Podle stupně rozptýlení bodů kolem křivky v Shepardovém diagramu můžeme považovat zvolený dvourozměrný model za uspokojivý (Obr. 7).

Dále se podíváme na hodnoty STRESSu pro různá nastavení počtu rozměrů. Při jednorozměrném řešení je hodnota STRESSu 0,258, u dvourozměrného řešení zaznamenáváme prudký pokles na hodnotu 0,103. Při dalším zvyšování počtu rozměrů je pokles STRESSu již méně výrazný (0,063 u tří rozměrů, 0,044 u čtyř a 0,029 u pěti; Obr. 8). Můžeme konstatovat, že námi zvolené nastavení NMDS se dvěma rozměry je dostatečné a kvalita modelu je dobrá.

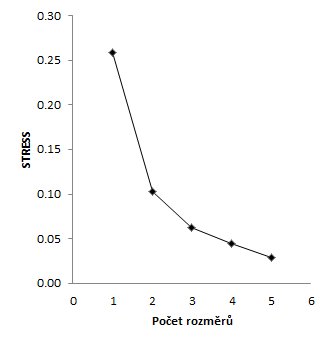Obr. 8: Hodnoty STRESSu pro různé nastavení počtu rozměrů redukovaného prostoru NMDS.