Metoda k-průměrů

Nejběžnější nehierarchickou metodou je metoda -průměrů. Hlavním cílem metody je nalezení takových skupin v mnohorozměrném prostoru, kdy vnitroskupinová podobnost je co největší. Princip vytvoření shluků je stejný jako při Wardově metodě: minimalizace celkové sumy čtverců vzdáleností uvnitř skupin. Výsledkem je vytvoření k skupin, které jsou od sebe co nejvíce odděleny.

Algoritmus metody je následující:

1. Zvolíme počáteční rozklad do shluků, nejčastěji náhodně. Podkladem ovšem může být také např. výsledek již provedeného shlukování, který chceme zlepšit.
2. Určíme centroidy pro všechny shluky v aktuálním rozkladu.
3. Postupně zhodnotíme pozici všech objektů. Pokud má objekt nejblíže k vlastnímu centroidu, neměníme jeho přiřazení ke shluku, jinak jej přiřadíme ke shluku, k jehož centroidu má nejblíže.
4. Centroidy každého z shluků jsou přepočítány.
5. Body 3 a 4 se opakují do té doby, kdy už žádný další přesun nezlepší kritéria. Tímto způsobem se v k skupinách objekty přesouvají tak, aby se minimalizovala variabilita uvnitř skupin a maximalizovala variabilita mezi skupinami (jde o relokační proceduru). Proces je tedy iterativní.

Tento algoritmus je základní, existuje ovšem i několik modifikací:

• Proces lze zahájit s vybranými objekty, které jsou zvoleny jako centroidy, místo počátečního rozkladu. Pak se dostáváme rovnou ke kroku č. 3. Další postup je již stejný.
• Přepočet centroidů lze provést po každém přesunu objektu (nikoli tedy jen po každém cyklu). Průběh shlukování a výsledek je pak závislý také na pořadí objektů, ve kterém vstupují do 3. kroku.

Nevýhodou metody -průměrů je, že pracuje se čtverci Euklidovských vzdáleností. To může být v některých případech problém, zejména při výskytu odlehlých objektů. Metoda -průměrů je citlivá na odlehlé hodnoty.

Další nevýhodou metody je nutnost definovat počet skupin předem. Je potřebné si uvědomit, že takto můžeme získat pouze lokální extrém, o kterém nemáme jistotu, že je zároveň extrémem globálním (Obr. 1). Proto je vhodné provést analýzu pro několik různých počtů skupin    a následně např. určit poměr vnitroskupinové a meziskupinové variability pro všechny analýzy (všechny ) a určit takový počet shluků , při kterém je poměr vnitroskupinové a meziskupinové variability nejmenší. Existuje řada dalších validačních metod pro určení optimálního počtu shluků, jimž se bude věnovat další kapitola.

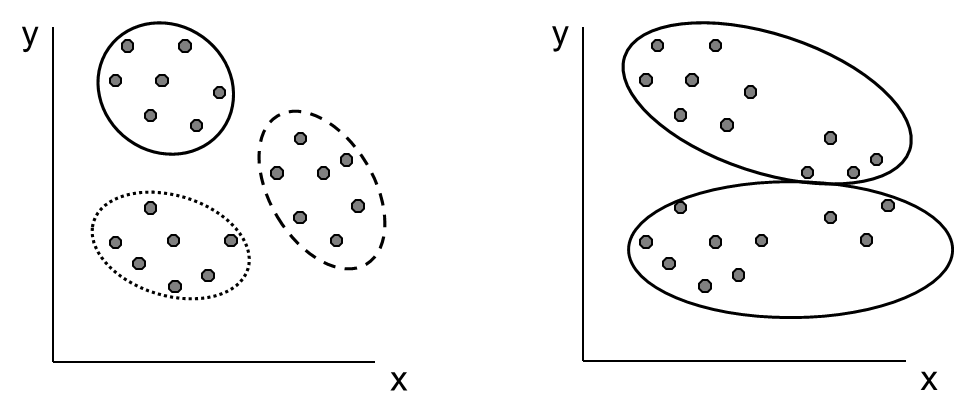Obr. 1: Ukázka rozdělení objektů do shluků nehierarchickou metodou k-průměrů. Výsledek je ovlivněn volbou počtu shluků. Vlevo: počet shluků je dobrá volba; vpravo: počet shluků je špatná volba.

Příklad 1
Metodu -průměrů představíme na příkladě 32 druhů savců a jejich zubních vzorců. Cílem úlohy je rozdělit savce do shluků právě podle jejich zubních vzorců (Tabulka 1). Analýzu jsme provedli v softwaru Statistica pro různé hodnoty , konkrétně

Tabulka 1: Zubní vzorce 32 druhů savců. hč = horní čelist, dč = dolní čelist.

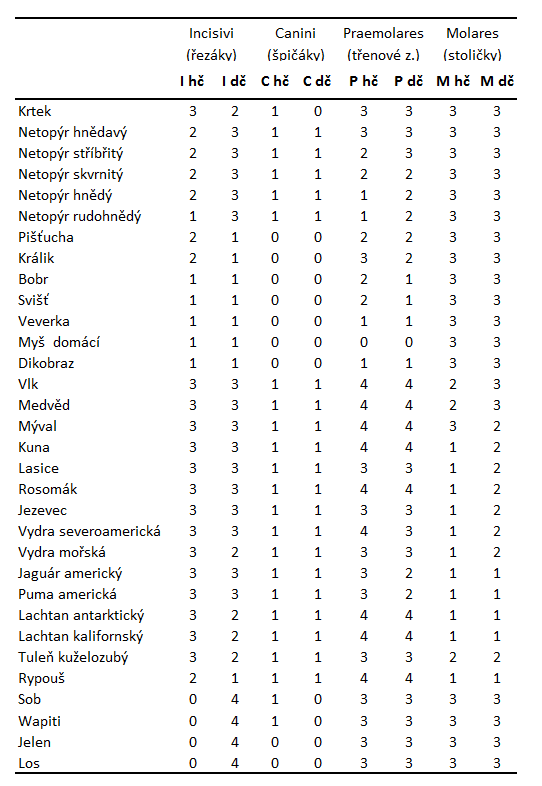
Výsledkem metody k-průměrů je zařazení jednotlivých druhů savců do dvou shluků v případě volby , do tří shluků pro , atd. až do devítí shluků pro (Tabulka 2).

Tabulka 2: Zařazení druhů savců do shluků vytvořených metodou k-průměrů pro , , . Výsledky jednotlivých analýz jsou uvedeny v příslušných sloupcích. Hodnoty v tabulce označují pořadové číslo shluku.

Při první analýze s definovanými dvěma shluky byl soubor savců rozdělen na dravce a ostatní savce. Při dělení souboru na tři shluky je jeden shluk tvořený dravci, druhý shluk kopytníky spolu s netopýry a třetí shluk ostatními savci. Velice vhodné se jeví rozdělení souboru na čtyři shluky - dravce, kopytníky, hmyzožravce (netopýry a krtek) a ostatní savce (hlodavci a zajícovci). Při nastavení s pěti shluky zůstává rozdělení savců do skupin stejné jako v případě čtyř shluků až na shluk dravců, který se rozdělil na dva shluky. Dělení souboru do šesti a více skupin je ze subjektivního pohledu zoologa již zbytečné a např. zařazení krtka s vlkem a medvědem do společného shluku těžko interpretovatelné. Samozřejmě subjektivní názor na počet shluků není dostatečný a proto je možno využít různé metody validace optimálního počtu shluků . Software Statistica poskytuje kromě zařazení objektů do shluků i hodnoty vzdálenosti objektů od centroidů a vzdálenosti mezi centroidy shluků, které mohou být užitečné pro spočítání validačního kriteria.

Jako nejvhodnějším podkladem pro rozhodnutí o počtu shluků se jeví použití některé z validačních metod pro stanovení optimálního počtu shluků v kombinaci s odbornými znalostmi a zkušenostmi vědce.