Zobecnění pro více tříd

Až dosud jsme předpokládali, že množina aproximovaných vektorů je konečná a že vektory nejsou, v případě klasifikační úlohy, rozděleny podle příslušnosti k jednotlivým klasifikačním třídám. Pro klasifikační úlohy je však členění vektorů základním předpokladem, proto se dále zabývejme, jak se změní podmínky, když vektory budou patřit do R klasifikačních tříd, které budou vymezeny jako části spojitého vektorového prostoru . Výskyt vektorů v jednotlivých klasifikačních třídách bude popsán podmíněnými hustotami pravděpodobnosti  a apriorní pravděpodobnost klasifikačních tříd bude , .

Za těchto podmínek bude autokorelační matice definována vztahem

(17)

a kovarianční matice buď podle předpisu

(18)

kde

(19)

nebo vztahem

(20)

když střední hodnota μ je vážený průměr středních hodnot určených podle vztahu (19) (obr.4a), tj.

(21)

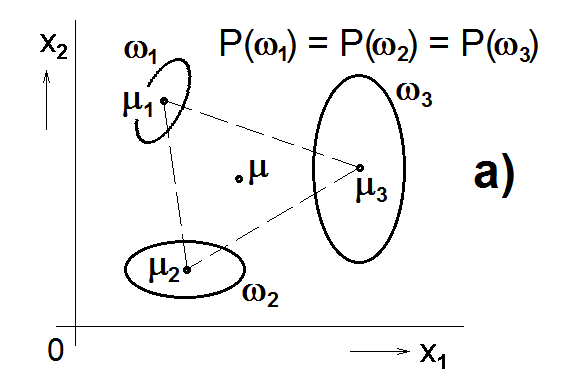
Výpočet kovarianční matice podle vztahu (18) bere ohled na střední hodnoty vektorů v jednotlivých klasifikačních třídách, vektory ze všech klasifikačních tříd se centrují podle středních hodnot vektorů v jednotlivých třídách (obr.4b). Klasifikační třídy se tedy po vycentrování mohou rozlišit pouze podle rozptylu ve směru jednotlivých souřadnicových os. Zato jsou transformované proměnné zcela nekorelované. Naopak výpočet kovarianční matice podle vztahu (20) centruje vektory podle celkové průměrné hodnoty, neodstraňuje vliv středních hodnot vektorů v jednotlivých klasifikačních třídách (obr.4c), a je proto lépe použít této definice v těch případech, kdy jsou střední hodnoty výrazně odlišné a nesou tak významnou část informace o klasifikační úloze.