Příklad 1

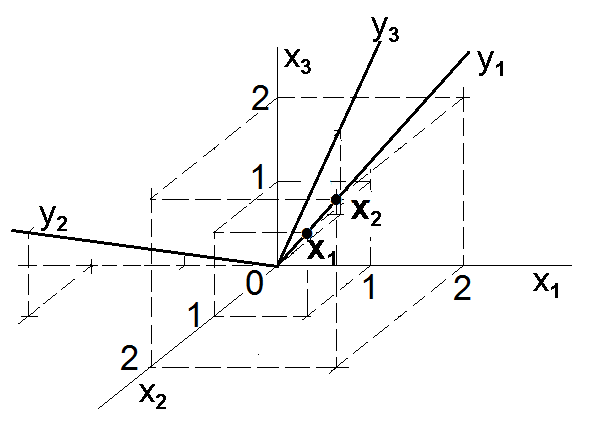
Předpokládejme, že množinu vektorů tvoří dva vektory  a (viz obr.5). Pomocí Karhunenova – Loevova rozvoje najděme novou souřadnicovou soustavu, která umožní popsat oba vektory s minimální střední kvadratickou odchylkou.

Řešení:
Jak lze usoudit z elementárního znění zadání a případně i ověřit z grafického vyjádření na obr.5, oba zadané vektory leží přesně na přímce dané směrovým vektorem . Proto by tento vektor měl být první hlavní komponentou, další dvě souřadnice již nejsou pro vyjádření obou zadaných vektorů podstatné.
Ověřme nyní tento intuitivní závěr výpočtem. Dle vztahu (8) pro výpočet autokorelační matice máme

Autokorelační matice o rozměru 3 x 3 má všechny tři řádky stejné, tj. jsou lineárně závislé. Vlastní čísla , která vypočítáme ze vztahu

a tedy 

jsou a dvě násobná .

Protože hodnota vlastního čísla určuje střední kvadratickou chybu vyjádření daného vektoru při odstranění vlastnímu číslu odpovídající souřadnice (dané vlastním vektorem), znamená to, že i když odstraníme souřadnice dané vlastními vektory odpovídajícími vlastním číslům a a použijeme pouze souřadnici definovanou vlastním vektorem náležejícím číslu , jsou oba vektory a vyjádřeny naprosto přesně.

Z cvičných důvodů ale spočítejme směry všech tří vlastních vektorů , =1, 2, 3, které určíme ze vztahu

Pro dostáváme lineární soustavu tří rovnic

která obsahuje pouze dvě lineárně nezávislé rovnice a tedy její parametrické řešení je

Při volbě parametru odpovídá vlastnímu číslu vlastní vektor , jak jsme usoudili na základě geometrického rozboru úlohy. Pro vlastní čísla vypadá definiční soustava rovnic následovně

To znamená, že dvě rovnice jsou lineárně závislé a její parametrické řešení je

Parametry a volíme tak, aby vlastní vektory byly navzájem ortogonální, pro např. a , pak a pro např. a a tedy . V tom případě jsou všechny tři vlastní vektory navzájem ortogonální, každé jejich vzájemné skalární součty jsou rovny nule.
Jak už jsme uvedli dříve, odstraněním souřadnic daných vlastními vektory a a ponecháním pouze souřadnice definované vlastním vektorem se nedopustíme žádné chyby ve vyjádření zadaných vektorů a (oba vektory leží na souřadnicové ose dané vektorem a proto také obě vlastní čísla ).
Jak by vypadala situace v případě, že bychom odstranili souřadnici ? Protože body a leží na vrcholech krychlí s hranami o délce 1, resp. 2 protilehlých k počátku (obr.6), je jejich vzdálenost od počátku a tím i souřadnice ve směru rovna délce prostorové úhlopříčky, tj.  v případě vektoru x₁, resp. v případě vektoru . Protože je nová souřadnicová soustava ortogonální, promítaly by se oba vektory při odstranění osy  do počátku. A konečně, vzhledem k tomu, že chybu popisu vektorů  vyjadřujeme pomocí střední kvadratické odchylky, je tato chyba rovna

což je právě hodnota .