Slovník | Vyhledávání | Mapa webu
 
Analýza a hodnocení biologických datVícerozměrné metody pro analýzu a klasifikaci dat Podobnosti a vzdálenosti ve vícerozměrném prostoru Metriky pro určení vzdálenosti mezi dvěma množinami vektorů Deterministické metriky pro určení vzdálenosti mezi dvěma množinami vektorů
Logo Matematická biologie

Metoda průměrné vazby

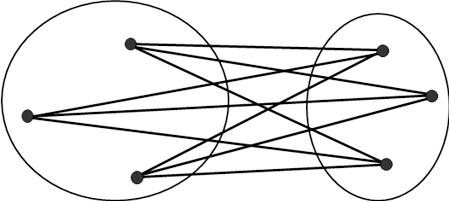
Metoda definuje vzdálenost dvou množin a pomocí průměrné vzdálenosti mezi všemi vektory obou množin (Obr. 6). Obsahuje-li množina P vektorů a množina Q vektorů, pak jejich vzdálenost podle metody průměrné vazby je určena vztahem
(64)

Tento způsob výpočtu často vede k podobným výsledkům jako metoda nejvzdálenějšího souseda.

Obr. 6: Vzdálenost dvou množin u metody průměrné vazby (podle [3]).

Příklad 7.6

Předpokládejme opět vektory vektory x1 = (0, 0), x2 = (10, 10),  x3 = (8, 8),  x4 = (6, 7), x5 = (4, 3) a x6 = (3, 2) rozdělené do dvou množin = {x1, x5, x6} a  = {x2, x3, x4}. Jaká je vzdálenost obou množin podle metody průměrné vazby, přičemž vzdálenost mezi jednotlivými vektory určujeme znovu pomocí Hammingovy metriky.

Řešení:

Vzdálenosti vektoru x1 od vektorů množiny jsou d(x1,x2) = 20, d(x1,x3) = 16 a d(x1,x4) = 13. Vzdálenosti vektoru x5 od vektorů množiny jsou d(x5,x2) = 13, d(x5,x3) = 9 a d(x5,x4) = 6. Konečně, vzdálenosti vektoru x6 od vektorů množiny jsou d(x6,x2) = 15, d(x6,x3) = 11 a d(x6,x4) = 8. Vzdálenost obou množin tedy je                   

 
vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity