
Vícerozměrné normální rozdělení
Použitelnost a také interpretovatelnost mnohých metod a postupů je závislá na splnění předpokladu normálního rozdělení sledovaných proměnných. Pokud je předpoklad splněný, metody založené na tomto předpokladu mohou využít kompletní matematický aparát schovaný za danou statistickou metodou, což je velmi výhodné. Tyto metody jsou také relativně snadno pochopitelné a se získanými řešeními se dobře pracuje. Ovšem v reálném světě bývá často obtížné předpoklad o normálním rozdělení dodržet, drobné odchylky od vícerozměrné normality však nejsou problémem.
Ověřením vícerozměrné normality se budeme zabývat podrobněji v následující kapitole, nyní se proto věnujme samotnému vícerozměrnému rozdělení. Vyjděme z jednorozměrného normálního rozdělení, jehož hustota má tvar
|
|
(6) |
kde μ je střední hodnota proměnné x a σ2 je její rozptyl. V exponentu je čtverec vzdálenosti , tedy vzdálenosti x od střední hodnoty μ, kde jednotkou vzdálenosti je směrodatná odchylka σ.
Vícerozměrné normální rozdělení je rozšířením jednorozměrného normálního rozdělení pro více než jednu proměnnou (p ≥ 2). Náhodný vektor x má vícerozměrné normální rozdělení, má-li jeho hustota pravděpodobnosti tvar
|
|
(7) |
kde je vektor p středních hodnot (vektor výběrových průměrů) proměnných a
je kovarianční matice proměnných.
Pro vícerozměrné normální rozdělení můžeme chápat kvadratickou formu v exponentu jako čtverec vzdálenosti vektoru x od vektoru μ, ve kterém je obsažena informace z kovarianční matice:
|
|
Ve skutečnosti jde o tzv. Mahalanobisovu vzdálenost vektoru x od vektoru μ, jež bude podrobněji popsána v kapitole věnované metrikám pro určení vzdálenosti mezi dvěma vektory s kvantitativními hodnotami souřadnic , přičemž má chí-kvadrát rozdělení s p stupni volnosti, tedy
. Geometricky se jedná o povrch elipsoidu (ve dvourozměrném případě elipsu) se středem μ a osami
, j = 1, 2, … p, kde
jsou vlastní čísla a vj vlastní vektory matice Σ.
Speciálním případem vícerozměrného normálního rozdělení je dvourozměrné normální rozdělení (tedy pro p = 2). Mějme dvě proměnné x1 a x2 se středními hodnotami μ1 a μ2, rozptyly ,
a kovariancí σ12. Vektor středních hodnot je tedy μ=(μ1,μ2)T a kovarianční matice
. Hustotu dvourozměrného normálního rozdělení pak můžeme vyjádřit ve tvaru
|
|
(9) |
kde ρ je korelační koeficient definovaný jako . Determinant kovarianční matice Σ lze pak vyjádřit jako
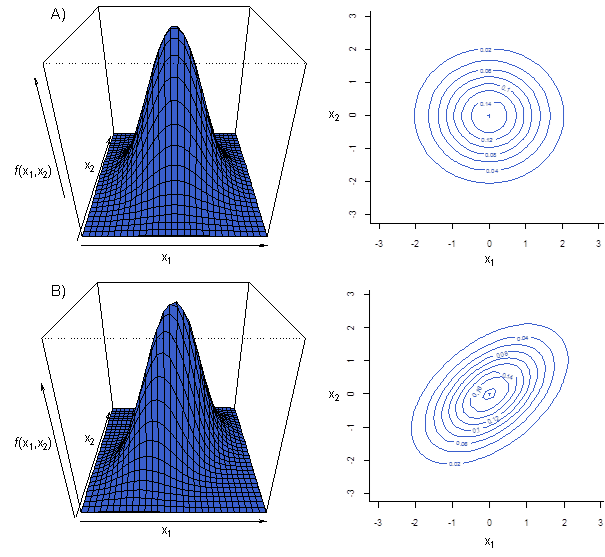
, přičemž tento determinant je roven nule, když ρ = 1. Pro dvourozměrné normální rozdělení můžeme hustotu rozdělení a elipsy konstantní hustoty znázornit graficky (Obr. 1).
Na závěr si uveďme vlastnosti vícerozměrného normálního rozdělení:
- lineární kombinace složek vektoru x mají normální rozdělení;
- všechny podmnožiny x mají normální rozdělení;
- nekorelovanost náhodných proměnných z x znamená jejich nezávislost;
- všechna podmíněná rozdělení jsou normální.
Tyto vlastnosti se využívají při odvozování mnoha metod pro analýzu vícerozměrných dat.




