Poměr rozptylů

Jak bylo dříve uvedeno, pro klasifikaci jsou výhodnější ty proměnné, pro které je menší rozptyl obrazů uvnitř klasifikačních tříd a současně co největší vzdálenost (rozptyl) mezi třídami. To znamená, že se lze při selekci proměnných řídit hodnotami poměru rozptylu mezi třídami vzhledem k rozptylu uvnitř tříd. Čím větší bude tento poměr, tím méně pravděpodobná bude chyba klasifikace, a tím také bude lépe proveden výběr proměnných.

Ke stanovení zmíněného poměru je třeba charakterizovat oba použité rozptyly. Rozptyl uvnitř R tříd lze obecně charakterizovat disperzní maticí (v případě řádkových vektorů)

kde

Příklad 1

Předpokládejme tři množiny (klasifikační třídy) obsahující vektory:

množina :  = (3, 0, 0),  = (3, 1, 0), = (3, -1, 0);

množina :  = (0, 1, 0),  = (0, 3, 0);

množina :  = (0, -1, 2), = (0, 0, 2),  = (0, 1, 2).

Dále, nechť jsou vektory ve svých množinách zastoupeny rovnoměrně, tj. _,  a  a apriorní pravděpodobnosti jednotlivých množin nechť jsou _, a . Určete disperzní matici podle vztahů (1) a (2).

Řešení:

Střední vektory jsou podle vztahu (2)  = (3, 0, 0),  = (0, 2, 0) a  = (0, 0, 2). Protože se jedná o diskrétní případ, přechází vztah (1) z integrálního na sumační

Za těchto podmínek jsou dílčí disperzní matice pro jednotlivé množiny

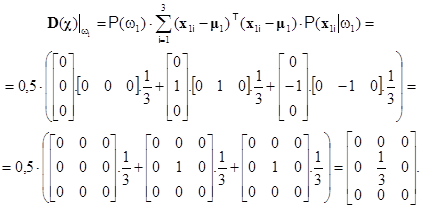
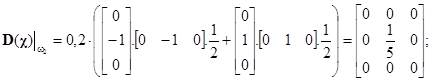
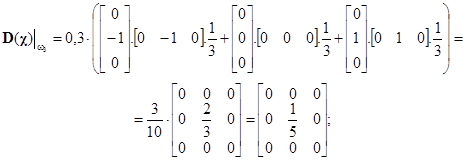
Pro určení výsledné disperzní matice sečteme tři dílčí matice

                                                                                                                                               †

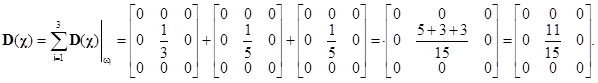
Rozptyl mezi třídami může být definován např. vztahem

kde .

Příklad 2

Pro zadání z příkladu 1 určete podle vztahu (3) matici popisující rozptyl mezi třídami.

Řešení:

Střední vektory jsou podle vztahu (2)  = (3, 0, 0),  = (0, 2, 0) a  = (0, 0, 2) a jejich rozdíly

Výsledná matice pak je

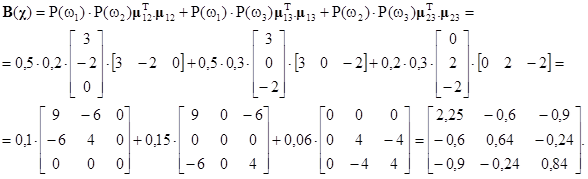
Pokud

můžeme také psát

Jestliže je disperzní matice regulární, tj. jestliže má inverzní matici, pak lze vyjádřit vlastnosti výskytu vektorů v prostoru při zvolené kombinaci hodnot proměnných, např. vztahem

Další možné používané způsoby popisu rozptylových vlastností vektorů jednoduchým parametrem jsou

Příklad 3

Pro zadání z příkladu 1 vyberte vhodný z kriteriálních vztahů (6) až (8) a vypočítejte jeho hodnotu.

Řešení:

Matice není regulární – její hodnost je menší než počet řádků, resp. její determinant je nulový. Proto lze použít pouze vztah (7).

Stopa matice je rovna součtu prvků hlavní diagonály, tj.  = 1/3 = 0,33 a stopa matice je  = 3,73. Z toho  = 1,243.
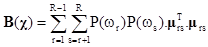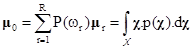
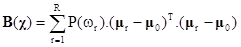
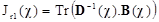
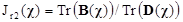
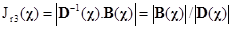