
Metoda nejvzdálenějšího souseda
Je založena na přesně opačném principu než obě předcházející metody. Platí, že
|
|
(62)
|
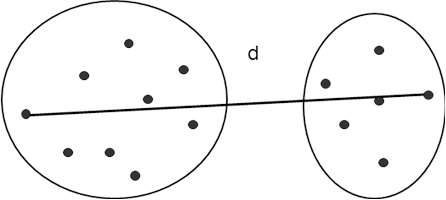
tedy vzdálenost mezi dvěma množinami je dána maximální vzdáleností mezi všemi možnými zástupci obou množin (Obr. 5). Generování protáhlých struktur tato metoda potlačuje, naopak vede k tvorbě nevelkých kompaktních množin.
Tak jako v předcházejícím případě je možné i zobecnění použitím k nejvzdálenějších vektorů z obou shluků, pak platí
|
|
(63)
|
Příklad 7.4
Předpokládejme stejné zadání jako v příkladu 7.2, tj. že na vstup shlukovacího algoritmu přivedeme vektory x1 = (0, 0), x2 = (10, 10), x3 = (8, 8), x4 = (6, 7), x5 = (4, 3) a x6 = (3, 2) v uvedeném pořadí. Vzdálenost mezi dvěma vektory bude určována pomocí Hammingovy metriky a rozhodnutí, zda vektory patří do téhož shluku, bude rovněž záviset na prahové hodnotě dmez = 7. Změnou nechť je, že vzdálenost mezi vektorem a shlukem budeme určovat na základě metody nejvzdálenějšího souseda.
Řešení:
Zpracování prvních tří vektorů je zcela stejné jako v příkladu 7.2. V této fázi řešení proto znovu existují dvě množiny = {x1} a
= {x2, x3}.
Pro x4 jsou vzdálenosti d(x4,x1) = 6 + 7 = 13 > dmez, d(x4,x2) = 4 + 3 = 7 a d(x4,x3) = 2 + 1 = 3. Nejvzdálenější soused vektoru x4 z druhého shluku je proto vektor x2, vzdálenost d(x4,x2) = dmez, tedy x4 zařadíme ještě do druhého shluku, který už v tomto okamžiku zahrnuje vektory = {x2, x3, x4}.
Pro vektor x5 je vzdálenost od prvního shluku, představovaného pouze vektorem x1, d(x5,x1) = 4 + 3 = 7 = dmez. Vzdálenosti od řetězců druhého shluku jsou d(x5,x2) = 6 + 7 = 13, d(x5,x3) = 4 + 5 = 9 a d(x5,x4) = 2 + 4 = 6. Podle kritéria nejvzdálenějšího souseda určuje vzdálenost vektoru x5 od shluku = {x2, x3, x4} vzdálenost d(x5,x2) = 6 + 7 = 13
dmez. Zařadíme jej proto k vektoru x1 do prvního shluku
= {x1, x5}.
Konečně pro poslední vektor x6 jsou vzdálenosti od vektorů prvního shluku d(x6,x1) = 3 + 2 = 5 a d(x6,x5) = 1 + 1 = 2. Obě vzdálenosti jsou menší než limitní hodnota dmez a větší z nich je d(x6,x1). Nejvzdálenější soused z druhého shluku je vektor x2, pro který je d(x6,x2) = 7 + 8 = 15 dmez. Vektor x6 tedy opět zahrneme do shluku
a je
= {x1, x5, x6}.
Ve srovnání s výsledkem příkladu 7.2 jsou shluky = {x1, x5, x6} a
= {x2, x3, x4} o poznání kompaktnější.
Příklad 7.5
Co by se stalo, pokud bychom v zadání příkladu použili mezní hodnotu dmez = 6?
Řešení:
Zadané vektory by se rozdělily do tří shluků = {x1, x6},
= {x2, x3} a
= {x4, x5}.




