Validační metoda siluety

Validační metoda siluety počítá hodnotu šířky siluety pro každý objekt, průměrnou hodnotu šířky siluety pro každý shluk a průměrnou hodnotu šířky siluety pro celý soubor. Tento přístup je založen na porovnání průměrné šířky siluety pro daný shluk. Silueta zde reprezentuje poměr podobnosti a odlišnosti od ostatních shluků. Průměrná šířka siluety může být použita k validaci shlukové analýzy a k rozhodnutí o vhodnosti zvoleného počtu shluků. K získání hodnoty použijeme vzorec

kde je průměrná odlišnost – tého objektu od všech ostatních vzorků ve stejném shluku, je minimum z průměrů odlišnosti – tého objektu ke všem shlukům. může nabývat hodnot . Když je hodnota siluety blízká jedné, znamená to, že objekt je zařazen do správného shluku, je-li hodnota siluety blízká nule, znamená to, že objekt můžeme zařadit také do jiného shluku, vzorek leží stejně daleko od obou shluků. Hodnota mínus jedna nám indikuje špatně zařazený objekt. Celková průměrná hodnota pro celý datový soubor je jednoduše průměr ze všech získaných .

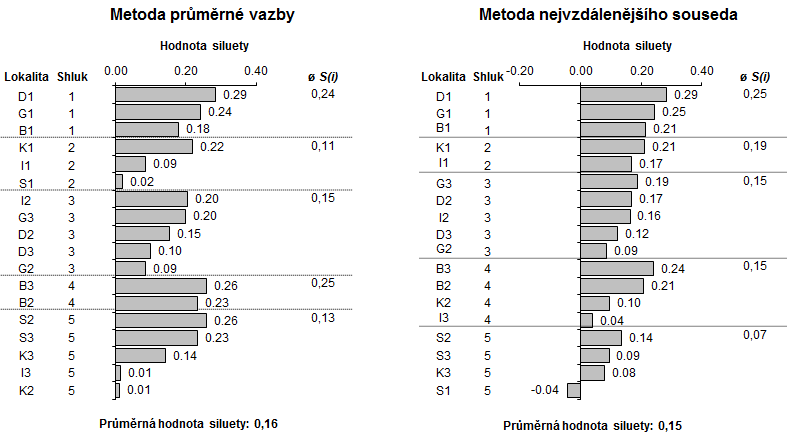
Největší hodnota celkové průměrné siluety indikuje nejlepší shlukování (počet shluků). Proto počet shluků s největší průměrnou hodnotou šířky siluety je optimální řešení. Výstupem této metody bývá sada grafů, kde jsou vyznačeny hodnoty siluety pro všechny objekty ve shlucích pro více variant shlukování (Obr. 3).

Příklad 4
V tomto příkladu si ukážeme výpočet validační metody siluety. Jako vstupní data použijeme data z příkladu 1 a 2 (tzn. data z  příkladu 1 z kapitoly Hierarchická shluková analýza). Výpočet vychází z Tabulka 1, kde se opět bude sledovat, která metoda nám nejlépe odpovídá struktuře dat. Pro ukázku výpočtu použijeme stejné dělení do pěti shluků a budeme sledovat, která metoda je podle siluety optimální. Vycházet budeme z Tabulky 2, která obsahuje asociační matici založenou na Euklidovské vzdálenosti a je seřazená dle příslušnosti lokalit do shluku dle metody nejvzdálenějšího souseda. Detailní výpočet si představíme na variantě vytvořené pomocí metody nejvzdálenějšího souseda (Tabulka 7).

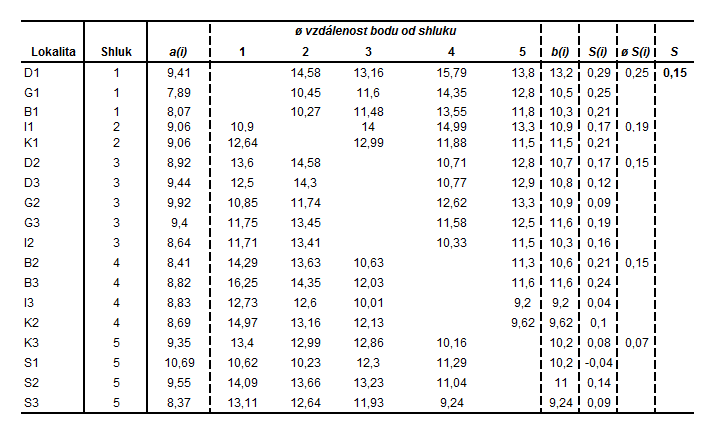
– průměr
– průměrná vzdálenost lokality od ostatních lokalit ve stejném shluku
– minimum z průměrných vzdáleností lokality od ostatních lokalit ve shluku, do kterého lokalita nepatří
– hodnota siluety
– průměrná hodnota siluety pro daný shluk
– celková průměrná hodnota siluety

Podle schématu z Tabulky 7 velmi snadno získáme hodnoty siluety i pro metodu průměrné vazby, výsledky jsou vykresleny na Obr. 3. Lze si všimnou lokality S1, která má u metody nejvzdálenějšího souseda zápornou hodnotu siluety. Tato hodnota nám indikuje špatně zařazený objekt. Podle výsledku z Obr. 3 zvolíme jako optimální variantu tu, která přestavuje největší hodnotu celkové průměrné hodnoty siluety. V našem případě se jedná o shlukovou analýzu založenou na metodě průměrné vazby.