Lineární verze metody podpůrných vektorů – lineárně neseparabilní třídy
Pokud nejsou třídy lineárně separovatelné, nemohou být podmínky 
představené v předchozí podkapitole splněny pro všechny body současně. Navíc i v některých případech, kdy jsou třídy lineárně separovatelné, by mohlo být výhodnější pár objektů raději klasifikovat chybně a vytvořit robustnější klasifikátor s větším tolerančním pásem, než vytvořit klasifikátor, který sice všechny trénovací objekty klasifikuje správně, ale bude mít velmi úzké toleranční pásmo a na nová data bude fungovat špatně, protože bude přeučený (případem je situace na Obr. 9 v minulé podkapitole).
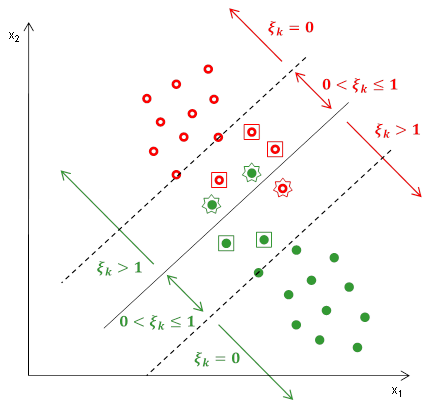
Tyto problémy lze vyřešit tak, že zavedeme relaxační proměnné (slack variables) 
vyjadřující, jak moc každý bod (objekt) porušuje danou podmínku (Obr. 10), tedy:
- pokud leží objekt vně tolerančního pásma a je správně klasifikován, pak
;
- pokud leží objekt uvnitř tolerančního pásma a je správně klasifikován (na Obr. 10 jsou tyto body ohraničeny čtverečky), pak
;
- pokud leží objekt na opačné straně hranice a je tudíž chybně klasifikován (na Obr. 10 jsou tyto body ohraničeny hvězdičkami), pak
.
Pomocí relaxačních proměnných tak můžeme podmínky elegantně zapsat ve tvaru
Obr. 10. Znázornění klasifikace metodou podpůrných vektorů se zavedením relaxačních proměnných. Objekty v tolerančním pásmu (dáno černými čárkovanými čarami) na správné straně hranice (černá čára) jsou vyznačeny čtverečky, chybně klasifikované objekty jsou označeny hvězdičkami.
Když teď chceme najít dělící přímku poskytující co nejrobustnější klasifikaci, musíme se snažit nejen maximalizovat šířku tolerančního pásma, ale také minimalizovat počet subjektů z trénovací množiny, které leží v tolerančním pásmu nebo jsou dokonce špatně klasifikovány (tj. těch, pro které
). To můžeme vyjádřit jako minimalizaci kriteriální funkce:
kde
a
C vyjadřuje poměr vlivu obou členů kriteriální funkce, přičemž pro vysoké hodnoty
C bude počet trénovacích subjektů v tolerančním pásmu a počet chybně klasifikovaných trénovacích subjektů nízký, ale toleranční pásmo bude úzké, zatímco pro nízké hodnoty
C bude toleranční pásmo širší ovšem za cenu vyššího počtu objektů v tolerančním pásmu i počtu chybně klasifikovaných objektů (Obr. 11). Protože bohužel nevíme, jaká hodnota parametru
C je pro naše data nejvhodnější, volíme parametr
C zpravidla na základě
křížové validace]. Z
Obr. 11 navíc vyplývá, že podpůrnými vektory jsou u této verze metody podpůrných vektorů nejen ty objekty, které leží na hranici tolerančního pásma, ale i objekty, které leží v tolerančním pásmu a jsou správně klasifikovány (
), a rovněž objekty, které leží na opačné straně hranice (
).
Obr. 11. Ilustrace šířky a počtu podpůrných vektorů při různých hodnotách parametru C.
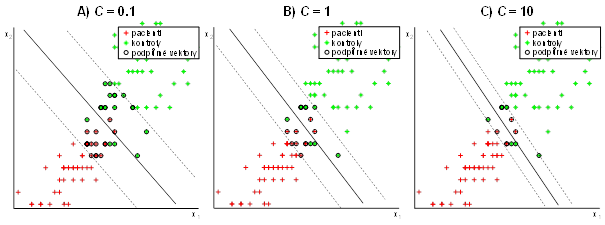
Ve tvaru (28) by však bylo obtížné kriteriální funkci minimalizovat, proto se používá jiný tvar:
Tuto úlohu za podmínky (27) lze také řešit pomocí metody Lagrangeova součinitele. Zavedeme vektor Lagrangeových součinitelů 
, kde 
, a pomocí nich vyjádříme optimalizovanou funkci jako:
za podmínek
Toto Lagrangeovu funkci zderivujeme podle proměnných 
a 
, 
a derivace položíme rovny nule, čímž získáme soustavu (tzv. Karushovy – Kuhnovy – Tuckerovy podmínky):
Po zderivování získáme:
|
|
|
|
|
|
 pro  , |
|
což je opět soustava (nelineárních) rovnic. Řešením této soustavy získáváme optimální hodnoty pro a .
Obdobně jako u lineárně separabilních tříd můžeme dosadit výrazy (37) a (38) do výrazu (30), čímž dostaneme
tedy výraz analogický k výrazu (26). U nelineárně separabilních tříd však funkci (40) maximalizujeme za podmínek 
pro a
. Této formy zápisu opět využijeme v podkapitole o nelineární verzi metody podpůrných vektorů.
