Princip
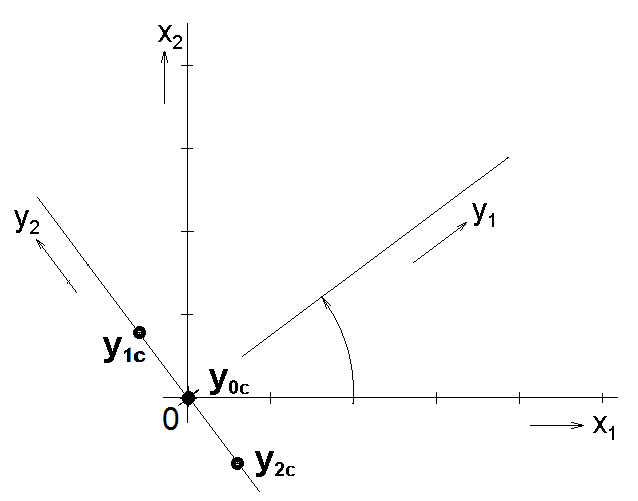
Představme si úlohu, kdy jsou reálné objekty popsány vektory ve dvourozměrném prostoru (se dvěma souřadnicemi a
), např. tak, jak je zobrazeno na obr.1. Nyní se pokusme vyjádřit dané vektory v jiné souřadnicové soustavě, jejíž souřadnice
a
jsou dány lineární kombinací těch původních
a
. To znamená, že v tomto dvourozměrném případě platí
|
|
(1)
|
 |
Důsledkem takovéto lineární transformace je, že nová souřadnicová soustava ,
je oproti původní
,
pouze otočená kolem počátku. Velikost otočení bude závislá na hodnotách parametrů
,
,
a
. Aby byla nová souřadnicová soustava pravoúhlá (ortogonální), stejně jako původní, je nutné, aby byl skalární součin transformačních vektorů
a
nulový. Je současně užitečné (nemá-li dojít k prodloužení, resp. zkrácení měřítka na osách), aby byly oba transformační vektory normované, tj. aby velikost jejich modulu byla jednotková.
Mějme v původním prostoru zobrazeném na obr.1 bod o souřadnicích = (4, 3). Nová soustava nechť je určena transformačními vztahy
Ověřte ortogonalitu transformačních vztahů a určete souřadnice bodu v nové souřadnicové soustavě.
Řešení:
Skalární součin transformačních vektorů . Transformace je proto ortogonální. Transformační vektory jsou i normované, protože jejich moduly jsou rovny
.
Souřadnice bodu = (4,3) v nové souřadnicové soustavě jsou
Můžeme tedy psát = (5, 0).
|
Poznámka: Zřejmě je na tomto místě vhodné připomenout a zdůraznit, že poloha bodu |
|
|
|
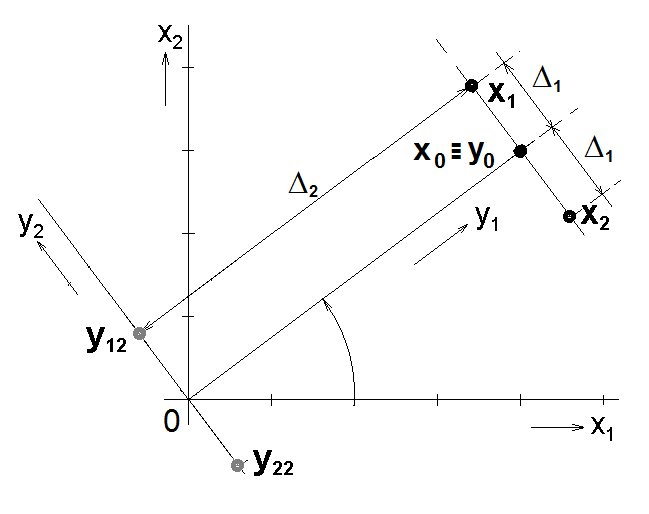
Obr.2 :Princip analýzy hlavních komponent s centrovanou množinou bodů |
Protože hodnota druhé souřadnice vektoru je nulová, jinými slovy bod leží na ose první transformované souřadnice, stačila by pro přesné vyjádření polohy bodu v nové souřadnicové soustavě pouze hodnota první souřadnice. Toto je základ principu redukce počtu souřadnic založené na lineární transformaci souřadnic. Je-li bodů v prostoru více, nelze obecně očekávat, že by všechny ležely na přímce procházející počátkem, ale jsou nějak rozmístěny v prostoru tak, jako jsou např. na obr.1 body
a
. Nemůžeme tedy očekávat, že bude pro přesné vyjádření polohy všech bodů potřeba pouze jedna souřadnice. Můžeme se ale pokusit pootočit původní soustavu tak, aby dané body v prostoru byly v novém redukovaném prostoru vyjádřeny jednou souřadnicí co nejlépe. To „co nejlépe“ musí být vyjádřeno nějakým matematickým kritériem. V případě analýzy hlavních komponent je tím kritériem celková odchylka všech bodů/vektorů od redukované reprezentace, popsaná pomocí kritéria ve smyslu minimální střední kvadratické odchylky.
Pokud bychom při dané transformaci souřadnicového systému (viz obr.1 ) provedli redukci rozměru prostoru odstraněním souřadnice , promítly by se oba původní zobrazené body
a
do pozice bodu
a oproti původním pozicím obou těchto bodů by se jejich nový průmět lišil o
. To znamená, že střední kvadratická chyba by pro tyto dva body byla rovna
. Pokud bychom redukovali rozměr prostoru daný souřadnicí
, byla by odchylka původní polohy od nových průmětů
a
daná v obou případech hodnotou
a střední kvadratická chyba by byla
. Z geometrického srovnání z obr.1 je zřejmé, že větší chyby se dopustíme odstraněním souřadnice
.
Nyní zvažme častý případ, kdy jsou zpracovávaná data centrována, tj. od hodnot jejich souřadnic je odečtena jejich střední hodnota (obr.2).
|
Poznámka: Vždy a zejména při řešení klasifikačních úloh je třeba důkladně zvážit, zda centrování dat, tj. odečtení jejich střední hodnoty, neodstraní informaci, která je důležitá z hlediska cílů jejich zpracování. |
Souřadnice centrovaných vektorů v transformované soustavě jsou = (0, 0),
= (0, 1) a
= (0, -1), což znamená, že hodnoty první souřadnice
jsou ve všech případech nulové (tedy i rozptyl je nulový). Body jsou rozloženy na transformované ose
. Z geometrické představy podle obr.2 vyplývá, že k přesné reprezentaci bodů
,
a
bude stačit souřadnice
, která popisuje data ve směru největšího rozptylu. To je ale závěr naprosto opačný, než tomu bylo v původním zadání. Na druhé straně celkem logický – změnila se data, změnil se i způsob jejich reprezentace.
Jak by se dalo postupovat při určování nové, potencionálně redukovatelné souřadnicové soustavy? Vysvětleme si na kvazioptimálním iteračním postupu, který je sice názorný, nicméně nemusí vést k zcela nejlepšímu řešení. Prakticky jej lze použít v případě, kdy je datová množina příliš veliká.
Pomocí zvoleného optimalizačního algoritmu používajícího dané kritérium nalezneme tu transformovanou souřadnici (komponentu), která nejlépe splňuje zvolené optimalizační kritérium. V příkladu 1 je to zjevně souřadnice , u centrovaných dat je to souřadnice ve směru největšího rozptylu dat, tedy
. Po nalezení první hlavní komponenty je nalezena druhá, která nejlépe popisuje data ve smyslu minimální střední kvadratické odchylky po odstranění první komponenty a současně je k první komponentě kolmá (ortogonální). Algoritmus poté pokračuje, než jsou nalezeny všechny nové transformované souřadnice, přičemž sledujeme, zda už je či stále není splněna podmínka pro dostatečně malou chybu vyjádření původního vektoru.
Globální optimum zaručuje algoritmus vycházející z tzv. Karhunenovy-Loevovy transformace nebo tzv. rozkladu na singulární hodnoty (SVD – Singular Value Decomposition), případně rozklad na vlastní vektory a vlastní čísla, jehož teoretické zdůvodnění je popsáno v následující kapitole.