Úvod do klasifikace pomocí hranic

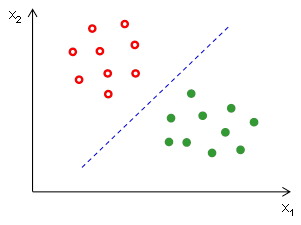
Vícerozměrná data můžeme znázornit v prostoru, v němž zobrazené body odpovídají jednotlivým objektům (či subjektům) a jehož dimenzionalita odpovídá počtu proměnných, kterými jsou objekty popsány. Pokud se v datech vyskytují skupiny objektů, které chceme od sebe oddělit, zřejmě nás intuitivně napadne nakreslit hranici, která bude prostor rozdělovat tak, aby byly na jedné straně od hranice objekty z jedné třídy a na druhé straně hranice objekty z druhé třídy (Obr. 1).

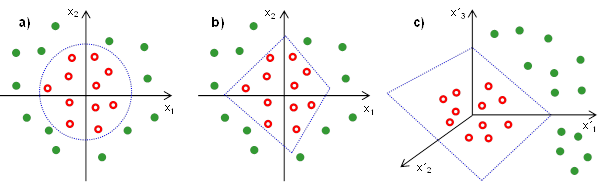
Hranice jsou tvořeny obecně nadplochami o rozměru o jednotku menší než je rozměr prostoru – v dvourozměrném prostoru je to tedy křivka (ve speciálním lineárním případě přímka), v trojrozměrném prostoru plocha (v lineárním případě rovina), atd. Způsoby určení oddělujících hranic závisí jednak na vlastnostech klasifikačních tříd a jednak na kritériích, která použijeme pro optimalizaci polohy hranic. Co se týče vlastností klasifikačních tříd, zajímá nás zejména:

• zda se jejich obrazy vyskytují v navzájem překrývajících se oblastech, či nikoliv – v tom případě hovoříme o separabilních či neseparabilních skupinách
• zda je možné skupiny objektů oddělit lineární hraniční plochou, či zda je vhodnější použít plochu nelineární.

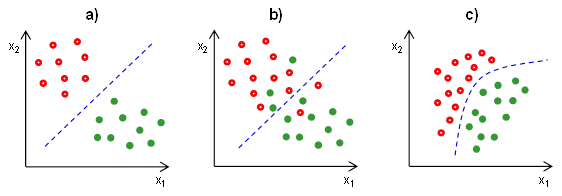
Na základě kombinací výše uvedených vlastností mohou nastat celkem tři situace, které jsou znázorněny na Obr. 2, tedy lineárně separabilní úloha, lineárně neseparabilní úloha s lineárně separovanými třídami a nelineárně separabilní úloha.

(1)

 

kde ) je tzv. váhový vektor,  je vektor hodnot proměnných popisujících klasifikovaný objekt či subjekt a absolutní člen posouvá hranici od počátku. Váhový vektor můžeme stanovit různými způsoby, z nichž si představíme Fisherovu lineární diskriminaci a také lineární verzi metody podpůrných vektorů. Dalšími metodami, které umožňují stanovení lineárních hranic, jsou metoda nejmenších čtverců či jednovrstvý perceptron, tyto metody však v těchto učebních textech nebudou rozebírány, protože jsou v praxi používány mnohem méně často než Fisherova lineární diskriminace a metoda podpůrných vektorů.

1. zachováme původní p rozměrný prostor a zvolíme nelineární hraniční funkci:

• definovanou obecně (např., nebo , nevýhodou je však obtížné rozhodování, jakou funkci máme použít (především ve vícerozměrném prostoru, který si nelze jednoduše vizualizovat), a nutnost stanovení parametrů takovýchto funkcí (v našem případě a, b a c); první problém se zpravidla řeší heuristicky pomocí apriorní informace o klasifikační úloze, druhý problém se stanovením parametrů hraniční funkce však vede na obtížně řešitelné nelineární optimalizační úlohy, proto se tomuto způsobu popisu klasifikačních tříd snažíme co nejvíce vyhýbat);
• složenou po částech z lineárních úseků (tzn. zjednodušíme stanovení parametrů hraniční funkce tím, že optimalizační úlohu parciálně linearizujeme, i když za cenu násobné realizace).

2. zobrazíme původní rozměrný prostor nějakou nelineární transformací do nového m rozměrného prostoru (obecně je ) tak, aby v novém prostoru byly klasifikační třídy lineárně separabilní, a v novém prostoru použijeme lineární klasifikátor. Tento přístup si probereme detailněji na příkladu nelineární verze metody podpůrných vektorů.