Lineární verze metody podpůrných vektorů – lineárně separabilní třídy
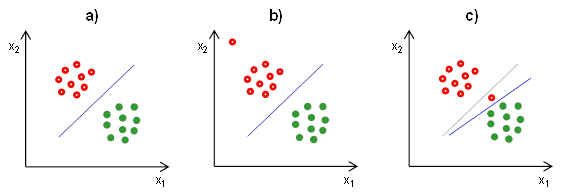
Pokud jsou klasifikační třídy lineárně separabilní, existuje nekonečně mnoho hranic, které dokáží rozdělit prostor tak, aby na jedné straně hranice byly pouze objekty (či subjekty) z jedné třídy a na druhé straně hranice pouze objekty z druhé třídy. Ilustrace několika možných hranic je uvedena na Obr. 7. Všechny přímky splňují požadavek na dokonalé oddělení obou skupin, lze však intuitivně odhadnout, že některá z přímek je vhodnější, jiná méně. Zřejmě nejlepší volbou je přímka, která je vyznačena silnější čárou, protože prochází v dostatečné vzdálenosti od objektů obou skupin. Takové řešení je nepochybně i nejrobustnější pro klasifikaci nových objektů, které nejsou součástí trénovací množiny.
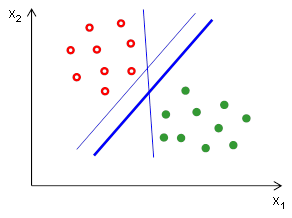
Abychom shrnuli předchozí poznatky, metoda podpůrných vektorů se snaží najít mezi všemi možnými hraničními nadrovinami (ve dvourozměrném případě přímkami) takovou, která rozděluje objekty do dvou požadovaných tříd co nejrobustněji - tj. takovou, která prochází v co největší vzdálenosti od objektů z obou tříd. Zopakujme si, že hranice je obecně definovaná jako:
|
|
(12)
|
Orientaci dělící přímky si tedy označíme vektorem a její polohu
. Klasifikace subjektu
do třídy
(resp.
) bude dána tím, jestli je výraz
větší (resp. menší) než 0. Konkrétně:
| pokud |
(13)
|
| pokud |
(14)
|
Vzdálenost bodu od hranice je dána vztahem
, kde
je velikost vektoru
. Změna velikosti tohoto vektoru nijak neovlivní výslednou klasifikaci, a tak si ji můžeme stanovit libovolně, například tak, aby pro nejbližší bod
ze třídy
byla hodnota výrazu
rovna +1 a pro nejbližší bod
ze třídy
byla hodnota výrazu
rovna -1. V tom případě máme na každé straně od dělící přímky toleranční pásmo o šířce
, ve kterém se nenachází žádný bod. Pro všechny body z trénovací množiny pak platí:
|
|
(15)
|
|
|
(16)
|
což můžeme stručněji zapsat jako
|
|
kde pro
ze třídy
a
pro
ze třídy
.
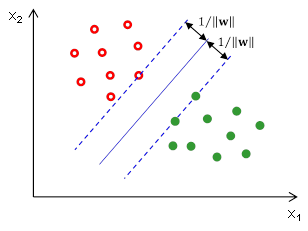
Abychom dosáhli co nejrobustnější klasifikace, budeme hledat takové hodnoty a
, aby byla celková šířka tolerančního pásma
co největší (Obr. 8). Hledat maximum funkce
je to stejné jako hledat minimum funkce
a toto minimum se nezmění, když kladnou hodnotu v čitateli umocníme na druhou (což nám zjednoduší výpočty). Takže dostáváme kriteriální funkci:
|
|
jejíž hodnotu se snažíme minimalizovat. Zároveň ale musí pro všechny body z trénovací množiny platit výše popsané podmínky (17).
Tuto podmíněnou kvadratickou optimalizační úlohu bychom dále řešili například pomocí metody Lagrangeova součinitele pro hledání vázaného extrému. Zavedeme vektor Lagrangeových součinitelů kde
,
a pomocí nich vyjádříme optimalizovanou Langrangeovu funkci jako:
|
|
za podmínek
|
|
(20)
|
Toto Lagrangeovu funkci zderivujeme podle proměnných a
a derivace položíme rovny nule, čímž získáme soustavu rovnic (tzv. Karushovy – Kuhnovy – Tuckerovy podmínky):
|
(21)
|
|
|
(22)
|
|
|
(23)
|
Po zderivování získáme:
|
|
|
|
|
což je opět soustava (nelineárních) rovnic. Řešením této soustavy pak získáváme optimální hodnoty pro a
.
Pokud bychom dosadili výrazy (24) a (25) do výrazu (19), dostaneme
|
|
což je funkce, kterou maximalizujeme za podmínek pro
a
. Této formy zápisu využijeme později v podkapitole o nelineární verzi metody podpůrných vektorů.
Povšimněme si, že pro výpočet orientace dělící přímky podle vztahu (24) jsou důležité jen ty body, pro které platí . Každý takový bod ovšem musí podle příslušné rovnice výše splňovat podmínku
, tedy musí ležet přesně na hranici tolerančního pásma (tzn. ve vzdálenosti
) a tedy pro něj platí
). Takovým bodům říkáme podpůrné vektory (odtud tedy název metoda podpůrných vektorů) a jen na nich závisí umístění dělící přímky. Říká se jim podpůrné z toho důvodu, že „podporují“ hranici tím způsobem, že pokud by se tyto objekty třeba jen nepatrně v prostoru pohnuly, pohne se i hranice. Ostatní objekty nemají na umístění hranice žádný vliv, takže pokud se pohne některý z ostatních objektů, umístění hranice se nezmění (ovšem za předpokladu, že se objekt nepřesune tak, že by byl blíž druhé klasifikační třídě než podpůrné vektory dané třídy, protože pak by se tento objekt stal podpůrným vektorem a umístění hranice by v tom případě ovlivnil).
Závislost klasifikátoru pouze na podpůrných vektorech, tedy objektech, které leží v sousedství s jinou skupinou, dělá z metody podpůrných vektorů robustní klasifikátor, protože nám nevadí, když mezi ostatními objekty bude odlehlá hodnota (Obr. 9b). V tom je rozdíl oproti Fisherově lineární diskriminaci, která počítá průměry a směrodatné odchylky na základě dat ze všech objektů z daných tříd, takže je na odlehlé hodnoty velmi citlivá.
Metoda podpůrných vektorů, jak jsme si ji teď přestavili (tzn. hledání minima výrazu (18) za podmínky (17)), však není robustní vůči odlehlým hodnotám, které leží ve směru ke druhé skupině, protože v tom případě je tato odlehlá hodnota podpůrným vektorem a tedy ovlivňuje umístění hranice (Obr. 9c). Proto se tato nejjednodušší verze metody podpůrných vektorů v praxi příliš nepoužívá a spíše se používá její verze se zavedením tzv. relaxačních proměnných, která je představena v následující podkapitole. Verze s relaxačními proměnnými umožňuje nejen výpočet metody podpůrných vektorů v případě lineárně neseparabilních tříd, ale i robustní výpočet hranice v případě lineárně separabilních tříd, protože umístění hranice není téměř vůbec ovlivněno odlehlými hodnotami.