Inverzní matice

Pro matice není definováno dělení. Tento formální nedostatek lze ale snadno obejít násobením tzv. inverzní maticí. Inverzní matice (značíme A^-1) má v tomto případě ekvivalentní význam jako převrácená hodnota čísla, kdy dělení dvou čísel  můžeme nahradit násobením .

K matici A existuje inverzní matice A^-1 pouze tehdy, pokud je matice A regulární.

Je-li , pak pro inverzní matici je

(11)

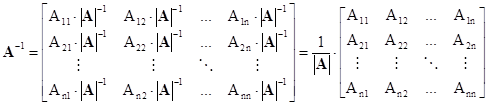kde |A| je determinant matice A a A_ij je doplněk prvku a_ij v determinant |A|.

Kromě definičního vztahu (11) lze k výpočtu inverzní matice použít i tzv. Gaussovu – Jordanovu eliminační metodu. Podle ní v prvním kroku výpočtu složíme matici B z původní zadané matice A a matice jednotkové I, tj. je

(12)

Poté se s elementárními operacemi popsanými v kapitole o hodnosti matice snažíme převést matici B do takového tvaru, kdy vlevo, místo prvků matice A, bude jednotková matice. V tom případě na pozicích jednotkové matice vpravo budou hodnoty prvků inverzní matice A^-1.

Příklad Matice.21:

Určete inverzní matici k matici .

Řešení:

Složená matice B má tvar . Upravíme ji následujícími operacemi:

• k druhému řádku přičteme první řádek;

• k třetímu řádku přičteme trojnásobek druhého řádku

;

• k prvnímu řádku přičteme trojnásobek druhého řádku

;

• druhý řádek vynásobíme (-1) a třetí řádek vydělíme 6

;

• od prvního řádku odečteme trojnásobek třetího řádku a druhý řádek sečteme s řádkem třetím

V této fázi výpočtu je levá polovina převáděné matice rovna jednotkové matici a tedy pravá polovina reprezentuje matici inverzní

.

Abychom ověřili správnost výpočtu inverzní matice, vynásobíme A.A^-1 a dostáváme, jak se sluší a patří

 

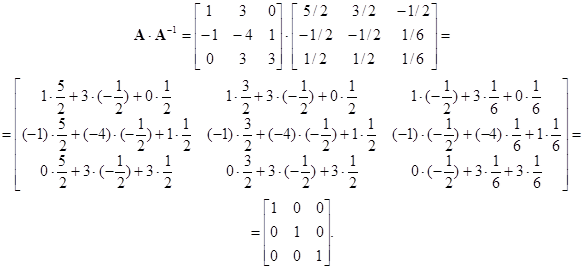
To znamená, že kontrolní výpočet vedl správně k jednotkové matici.                                   

 

Pro inverzní matici, případně její determinant dále platí:

• |A^-1| = 1/|A|;
• [A^-1] ^-1 = A;
• [A^T]^-1 = [A^-1]^T;
• [A.B]^-1 = B^-1. A^-1;
• pro symetrickou matici, tj. takovou, pro kterou je A^T = A, platí [A^-1]^T = A^-1;
• když A^-1 = A^T, je matice A ortogonální, tj. skalární součin každých jejích dvou různých řádků, resp. sloupců je roven nule, skalární součin každého řádku (sloupce) takové matice se sebou samým je roven jedné.

Kromě náhrady dělení lze inverzní matici použít i pro řešení soustavy lineárních algebraických rovnic.

Je-li matice A soustavy rovnic čtvercová a regulární, pak lze řešení x soustavy rovnic A.x = b

získat pomocí matice, která je inverzní k matici A, protože platí, že x = A^-1.b.

Pokud je matice A obdélníková, lze k ní sestrojit tzv. pseudoinverzní matici. Jejích definic je více a mají poněkud komplikovanější pozadí, proto se na tomto místě omezme pouze na konstatování, že lze najít i jistý ekvivalent inverzní matice za předpokladu, že je zadaná matice obdélníková.