Operace s maticemi

.

(2)

Příklad Matice.11

Vynásobte symetrickou matici  pěti.

Řešení:

.

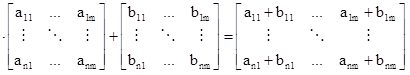(3)

Příklad Matice.12

Sečtěte matice  a .

Řešení:

Obě matice jsou téhož rozměru, proto je můžeme sečíst.

.

Pro násobení matice číslem a sčítání matic téhož rozměru (typu) platí:

1. A + (B + C) = (A + B) + C;
2. A + B = B + A;
3. A + 0 = A, kde 0 je nulová matice;
4. Pro matice A a B existuje právě jedna matice C taková, že A + C = B. Matici C určíme podle vztahu C = B + (-1).A = B – A.
5. k.(A + B) = k.A + k.B; (k + m).A = k.A + m.A.

,

(4)

To znamená, že řádky matice A násobíme sloupci matice B. Matice A tedy musí mít právě tolik sloupců, jako matice B řádků.

Příklad Matice.13

Vynásobte matice  a .

Řešení:

Protože matice A má rozměr (2,3) a matice B rozměr (3,2), bude mít matice C = AB rozměr (2,2). Pro její prvky je:

c₁₁ = a₁₁b₁₁ + a₁₂b₂₁ + a₁₃b₃₁ = 1.1 + 0.0 + 2.2 = 5

c₂₁ = a₂₁b₁₁ + a₂₂b₂₁ + a₂₃b₃₁ =0.1 + (-1).0 + 1.2 = 2

c₁₂ = a₁₁b₁₂ + a₁₂b₂₂ + a₁₃b₃₂ = 1.0 + 0.(-1) + 2.1 = 2

c₂₂ = a₂₁b₁₂ + a₂₂b₂₂ + a₂₃b₃₂ = 0.0 + (-1).(-1) + 1.1 = 2

To znamená, že .

Příklad Matice.14

Dokažte, že součin matice a matice k ní transponované je matice symetrická.

Skryté řešení:

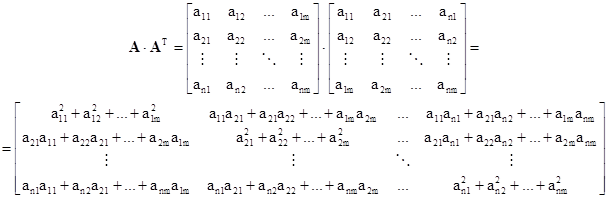
Ve vytvořené součinové matici je a_ij = a_ji pro všechna i ≠ j, což je definiční vlastnost symetrické matice.

Pro násobení matic A, B, C platí:

1. (AB)C = A(BC);
2. (A + B)C = AC + BC; A(B + C) = AB + AC
3. AB ≠ BA – o součinu AB hovoříme, že matici A násobíme maticí B zprava a naopak, matici B násobíme maticí A zleva; existuje-li součin matic A a B, nemusí existovat součin matic B a A;
4. AI = IA =A;
5. druhá mocnina matice A, tedy AA nebo A² existuje jen, když je matice A čtvercová;
6. (AB)^T = B^TA^T a obecně (ABCD…) = … D^TC^TB^TA^T.

Příklad Matice.15

Dokažte, že A + 0 = A.

Skryté řešení:

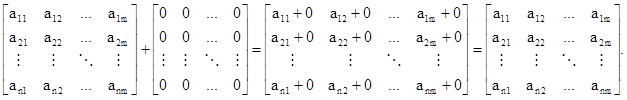
Příklad Matice.16

Dokažte, platí obecně AI = IA =A.

Skryté řešení:

Ekvivalentně lze postupovat pro důkaz IA =A.