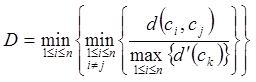Dunnův validační index
Tento index je založen na předpokladu, že nalezené shluky jsou kompaktní a dobře oddělené. Pro všechny oddělené shluky, kde představuje
– tý shluk, je Dunnův validační index počítán podle vzorce:
|
|
(1)
|
kde představuje minimální vzdálenost mezi shluky
a
(mezishluková vzdálenost),
je maximální vzdálenost uvnitř shluků,
je počet shluků. Minimum je počítáno pro všechny shluky, které byly získány. Dunnův index je tedy poměr nejmenší mezishlukové vzdálenosti k největší vnitroshlukové vzdálenosti. Nabývá hodnot od 0 do nekonečna a vysoké hodnoty indexu indikují optimální počet shluků.
Příklad 1
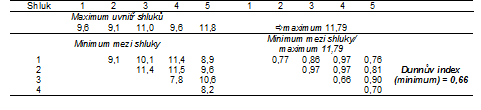
Výpočet Dunnova validačního indexu si představíme na konkrétním případu: jako vstupní data použijeme data z příkladu 1 z kapitoly Hierarchická shluková analýza . Na začátku si ukážeme výpočet Dunnova indexu pro metodu nejvzdálenějšího souseda. Vycházíme z asociační matice, která je založena na Euklidovské vzdálenosti. Matici je potřeba doplnit o přiřazení objektů do shluků, zde bylo použito dělení do pěti shluků (Tabulka 1).
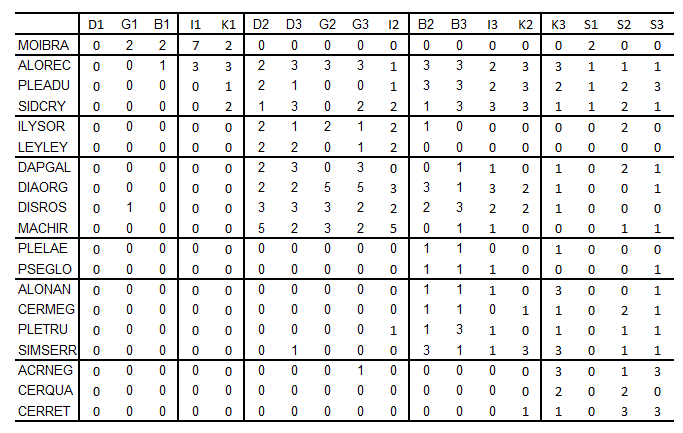
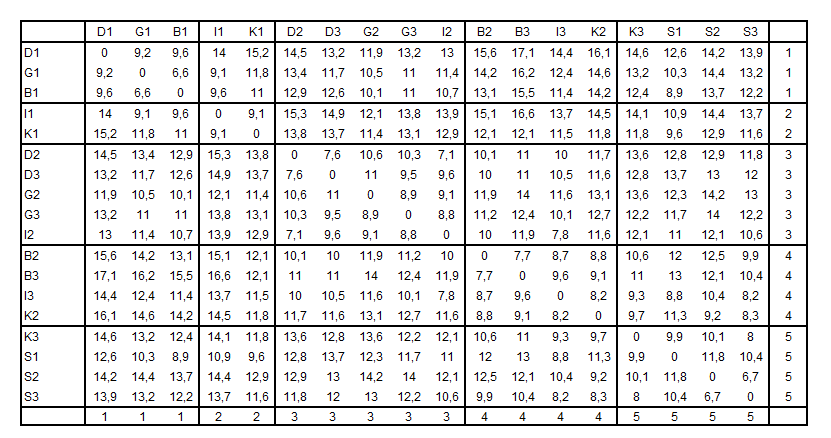
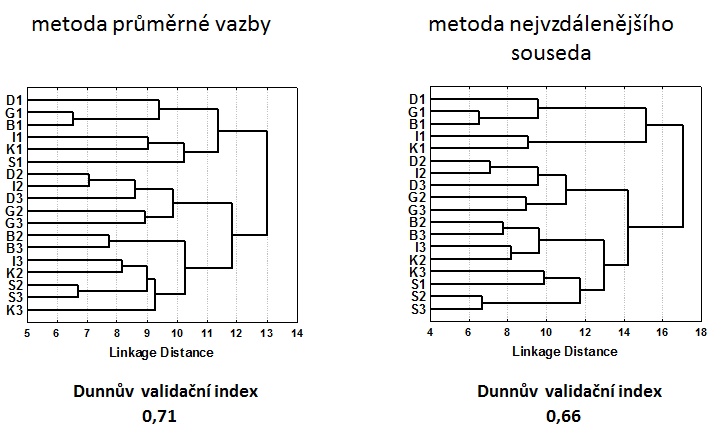
Pro snadnější výpočet asociační matici seřadíme dle příslušnosti lokalit do jednotlivých shluků (Tabulka 2). Pak zjistíme maximální vzdálenost mezi lokalitami v jednom shluku a minimální vzdálenost mezi lokalitami z odlišných shluků (Tabulka 3). Analogicky spočítáme Dunnův validační index i pro metodu průměrné vazby (Obr. 1). Dendrogram z metody nejbližšího souseda jsme nehodnotili, jelikož zde došlo k výraznému řetězení shlukovaných objektů (viz příkladu 1 z kapitoly Hierarchická shluková analýza). Podle hodnoty Dunnova indexu je nakonec vybrán ten postup shlukové analýzy, který vede k vyšší hodnotě. V tomto příkladu to je metoda průměrné vazby (Tabulka 1).
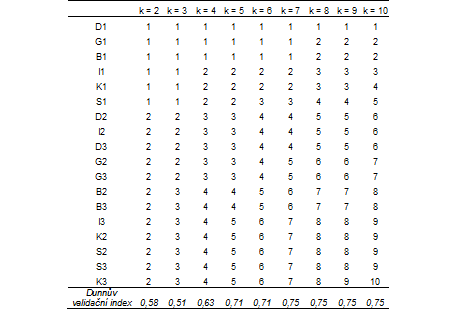
Příklad 2
V předchozím příkladu jsme si ukázali, jak se dají validační indexy použít pro výběr míry vzdálenosti mezi shluky. Ovšem validační indexy lze také použít pro rozhodnutí, do kolika shluků je nejlepší naše data rozdělit. Toto využití Dunnova validačního indexu si představíme na datech z předchozího příkladu. Nyní víme, že optimální míra mezi shluky je metoda průměrné vazby. Vybereme si tedy metodu průměrné vazby a budeme sledovat, do kolika shluků lze nejlépe daná data rozdělit. To znamená, že pro každý možný počet shluků získáme hodnotu Dunnova indexu. Největší hodnota z této množiny hodnot indikuje optimální počet shluků. Na ukázku provedeme výpočet pro počty shluků k = 2, k = 3, až k = 10. Pro výpočet můžeme použít software R, doplněný balíčkem „clValid“. Podle hodnot Dunnova validačního indexu (Tabulka 4) se zdá být optimálním počtem sedm shluků. Hodnota Dunnova validačního indexu je nejvyšší a počet objektů ve shlucích je rozumný. Při dalším dělení souboru (na 8, 9 a 10 shluků) zůstáva hodnota Dunnova indexu stejná.