
Úvod do hodnocení úspěšnosti klasifikace
V předchozích kapitolách jsme si představili jednotlivé metody používané pro klasifikaci dat. Proces klasifikace dat však nekončí výběrem klasifikační metody. Je nutné zjistit, jaká je úspěšnost klasifikace našich dat při použití dané klasifikační metody.
V ideálním případě máme k dispozici dvě datové sady, z nichž jednu použijeme k naučení (neboli natrénování) klasifikátoru a druhou k otestování, jak dobře klasifikátor klasifikuje. Natrénování klasifikátoru je např. vypočtení diskriminačních funkcí v případě Bayesova klasifikátoru, určení polohy hranice v případě Fisherovy LDA apod. Data použitá k natrénování klasifikátoru jsou označována jako „trénovací“ data, zatím data sloužící k otestování úspěšnosti klasifikátoru jsou nazývána jako „testovací“. V reálném vědeckém výzkumu však často nemáme dvě nezávislé datové sady (např. sadu pacientů se schizofrenií z Brna a z Prahy), proto náš jediný datový soubor musíme vhodným způsobem rozdělit na trénovací a testovací sadu, což je detailně popsáno v následující podkapitole. Zde budeme uvažovat termíny „trénovací“ a „testovací“ data bez ohledu na to, zda máme k dispozici dva datové soubory či jeden, protože princip hodnocení úspěšnosti klasifikace je ve všech případech stejný. Pro základní vysvětlení podstaty hodnocení úspěšnosti klasifikace budeme uvažovat klasifikaci subjektů do dvou tříd, a to pacientů a kontrol, všechny uvedené postupy však lze rozšířit vhodnými úpravami i na klasifikaci více tříd subjektů či objektů.
U testovacích dat je nutné, abychom znali skutečné správné zařazení subjektů či objektů do daných tříd. V tom případě můžeme srovnat výsledek klasifikace daných subjektů či objektů se skutečností a získat tzv. matici záměn (nebo též konfusní matici – confusion matrix), která je uvedena v Tab. 1. Matice záměn ukazuje:
- kolik výsledků rozpoznávání bylo skutečně pozitivních (TP – true positive), tedy kolik pacientů bylo správně klasifikováno jako pacienti,
- kolik výsledků rozpoznávání bylo falešně negativních (FN – false negative), tedy kolik pacientů bylo chybně klasifikováno jako kontroly,
- kolik výsledků rozpoznávání bylo skutečně negativních (TN – true negative), tedy kolik kontrol bylo správně klasifikováno jako kontroly,
- kolik výsledků rozpoznávání bylo falešně pozitivních (FP – false positive), tedy kolik kontrol bylo chybně klasifikováno jako pacienti.

Z vypočtených hodnot matice záměn lze následně získat základní míry hodnocení úspěšnosti klasifikace testovacích dat:
| celková správnost = |
(1)
|
| chyba = |
(2)
|
| senzitivita = |
(3)
|
| specificita = |
(4)
|
Celková správnost (accuracy) tedy udává podíl správně klasifikovaných subjektů ze všech testovacích subjektů. Chyba (error) naopak ukazuje podíl chybně klasifikovaných subjektů ze všech subjektů. Senzitivita (sensitivity) je podíl správně klasifikovaných pacientů ze všech pacientů, zatímco specificita (specificity) je podíl správně klasifikovaných kontrolních subjektů ze všech kontrol.
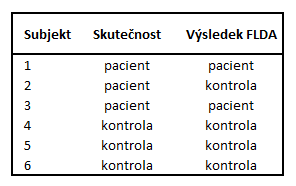
Vypočtěte celkovou správnost, chybu, senzitivitu a specificitu klasifikace 6 testovacích subjektů. Skutečné příslušenství těchto subjektů do tříd a výsledek klasifikace pomocí FLDA je uveden v následující tabulce:
Řešení
Vytvoříme nejprve matici záměn:

Následně spočítáme jednotlivé míry úspěšnosti klasifikace:
Celková správnost je 0,833, což znamená, že správně tedy bylo metodou FLDA klasifikováno 83,3% subjektů, zatímco špatně bylo klasifikováno 16,7% subjektů. Senzitivita 0,667 ukazuje, že bylo správně klasifikováno 66,7% pacientů. Specificita je rovna 1, což znamená, že byly správně klasifikovány všechny kontrolní subjekty.
K jednotlivým mírám úspěšnosti klasifikace můžeme vypočítat intervaly spolehlivosti. Ukážeme si výpočet intervalů spolehlivosti pro celkovou správnost. Pro ostatní míry úspěšnosti klasifikace se postupuje analogicky.
Jak již víme, celková správnost je podíl správně zařazených subjektů ze všech subjektů. Ze statistického hlediska tedy odhad pravděpodobnosti správného zařazení subjektů můžeme vyjádřit jako
|
(5)
|
kde je počet správně zařazených subjektů a je to veličina s binomickým rozdělením
a
je celkový počet subjektů. Za splnění předpokladů, že
,
a
, lze spočítat 95% interval spolehlivosti pro správnost pomocí aproximace na normální rozdělení:
|
(6)
|
Při klasifikaci 100 testovacích subjektů pomocí metody nejbližšího souseda byla získána celková správnost 78,0%. Vypočítejte 95% interval spolehlivosti (IS) pro tuto celkovou správnost.
Řešení
Při klasifikaci tedy byla získána celková správnost 78,0% (95% IS: 69,9% - 86,1%).




