Výběr popisných proměnných

Jak bylo uvedeno dříve, nedokážeme určit nejvhodnější veličiny z hlediska analýzy či klasifikace přímo, nýbrž pouze vybrat z předem dané množiny veličin. To znamená, že se objekt, reprezentovaný původně -rozměrným vektorem hodnot jednotlivých proměnných, snažíme vyjádřit vektorem m-rozměrným tak, aby množství tzv. diskriminační informace obsažené v původním vektoru bylo v co největší míře zachováno. Výběr proměnných se tedy převádí na hledání zobrazení , kterým se původní p-rozměrný prostor transformuje do nového m-rozměrného prostoru .

Zmenšení rozměru obrazového prostoru lze dosáhnout dvěma principiálně různými způsoby (Obr.2):

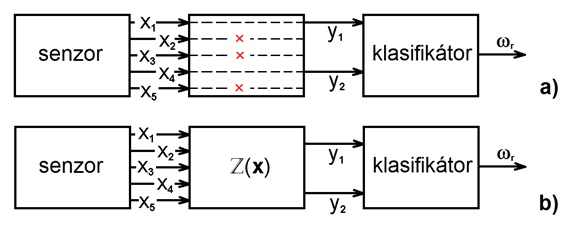
1. selekce – nalezení těch proměnných, které přispívají k separabilitě klasifikačních tříd nejméně, a pro klasifikaci se z původní množiny ponechá jen nejvíce informativních proměnných. Zobrazení  tedy pouze vynechává proměnných.
2. extrakce – transformace původních proměnných na menší počet jiných proměnných.

K tomu, abychom dokázali realizovat libovolný z obou způsobů výběru proměnných, je třeba definovat a splnit určité podmínky optimality.

Nechť je kriteriální funkce, jejíž pomocí vybíráme proměnné. Pak v případě selekce vybíráme vektor ze všech možných -tic proměnných , . Optimalizaci výběru proměnných tudíž můžeme formálně zapsat jako

Problémy, které je nutné vyřešit, jsou stanovení kriteriální funkce, rozměru nového prostoru a optimalizačního postupu.

Při extrakční alternativě transformujeme prostor na základě výběru zobrazení z množiny všech možných zobrazení z prostoru do , tj.

I v tomto případě je potřeba určit vhodnou kriteriální funkci, rozměr nového obrazového prostoru a rovněž zvolit požadavky na vlastnosti zobrazení i vhodný optimalizační postup (pokud nevyplývá z vlastností zobrazení).