Determinant

(5)

kde se součet provádí přes všechny permutace (k1,k2, …, kn) čísel 1,2, …, n a kde udává počet inverzí v permutaci (k1,k2, …, kn).

Abychom zcela objasnili výše uvedenou definici determinantu, bylo by ještě vhodné vysvětlit dva pojmy v ní uvedené – permutace a inverze v permutaci. Na druhé straně, při praktických výpočtech se tento obecný definiční vztah nepoužívá, nýbrž pouze jeho modifikace pro matice konkrétní velikosti. Pokud by stačila pouhá znalost dále uvedených konkrétních algoritmů výpočtu determinantu, lze následující orámovaný text vynechat.

Kombinatorický pojem permutace reprezentuje každou uspořádanou n-tici utvořenou z daných n různých prvků. Počet všech různých permutací množiny n prvků je n!. Příklad: Všechny permutace tří prvků 0, 1 a 2 (jejich počet je = 3.2.1 = 6) jsou (0,1,2), (0,2,1), (1,0,2), (1,2,0), (2,0,1) a (2,1,0). Je-li (p1,p2, …, pn) určitá permutace čísel 1, 2,…, n, pak říkáme, že dvojice čísel pj, pk (1 ≥ j,k ≥ n) tvoří v této permutaci inverzi, pokud . Lichý či sudý počet inverzí v permutaci určuje charakter (lichý, sudý) dané permutace.   Příklad: V permutaci (2,0,1) tvoří každá z dvojic (2,0) a (2,1) inverzi, protože a . Permutace má 2 inverze, je sudá.

Determinant matice 2. stupně určujeme podle vztahu (odvozeného z (5))

.

(6)

Příklad Matice.17

Determinant matice je                                                                                  

 

Determinant matice 3. stupně se určuje podle Sarrusova pravidla

.

(7)

Výpočet determinantu matic vyššího stupně než tři je založen na rozvoji vedoucímu ke snižování rozměru matice.

Pro determinant  platí rozvoj

|A| = a_i1A_i1 + a_i2A_i2 +…+ a_inA_in = (-1)ⁱ⁺¹a_i1|A_i1| + (-1)ⁱ⁺²a_i2|A_i2| +…+ (-1)ⁱ⁺ⁿa_in|A_in|.

Podle uvedeného rozvoje determinanty matic vyššího stupně než tři postupně rozložíme na determinanty o stupeň nižší a na stupeň třetí, který spočítáme podle Sarrusova pravidla. Při výpočtu pomocí rozvoje s výhodou využíváme prvků, v jejichž řádcích, resp. sloupcích, jsou nuly.

Příklad Matice.18

Určete hodnotu determinantu matice .

Řešení:

Matice A je 4. stupně, proto musíme hodnotu determinantu určit pomocí rozvoje. Pro rozvoj použijeme druhý sloupec, protože obsahuje pouze jeden nenulový prvek.

Se znázorněním úplného rozvoje je výpočet

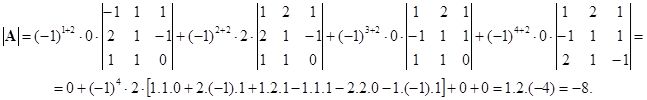
Pro determinanty platí následující vlastnosti:

1. hodnota determinantu se nezmění, pokud zaměníme jeho řádky za sloupce či naopak, tj. determinant matice a její matice transponované je týž, tj. |A| = |A^T|;
2. hodnota determinantu se nezmění, pokud k libovolnému řádku přičteme libovolnou lineární kombinaci jiných řádků;
3. zaměníme-li mezi sebou dva řádky (sloupce), determinant změní znaménko.
4. je-li řádek (sloupec) matice lineární kombinací jiného řádku (sloupce), je determinant roven nule;
5. determinant trojúhelníkové (diagonální matice) je roven součinu prvků v hlavní diagonále.

Pro operace s determinanty platí:

Pro součet determinantů je

(8)

a analogicky pro ostatní sloupce či řádky.

Příklad Matice.19

Určete hodnotu determinantu matice .

Řešení:

Determinant matice A lze vypočítat přímo pomocí Sarrusova pravidla

Variantou tohoto výpočtu je součtový rozklad determinantu |A| podle prvního řádku na

.

Protože první sčítanec obsahuje dva stejné řádky, je jeho hodnota nulová a hodnotu druhého determinantu lze opět určit podle Sarrusova pravidla

.

Pro násobení determinantu konstantou je

(9)

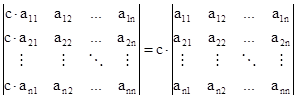a analogicky pro ostatní sloupce či řádky (když determinant násobíme konstantou, pak násobíme touto konstantou všechny prvky některého řádku či sloupce).

Pro násobení determinantů je

(10)

kde c_ij = a_i1b_1j + a_i2b_2j +…+ a_inb_nj, i,j = 1, 2, …, n.