Metriky pro určení vzdálenosti mezi dvěma vektory s kvalitativními hodnotami souřadnic

Použití konkrétní metriky závisí vždy na řešené úloze. Pokud se metrika používá pro klasifikaci, pak rozhodujícím kritériem pro posouzení vhodnosti té které metriky musí být kvalita výsledků klasifikace. Kromě tohoto základního kritéria lze při výběru možné metriky použít i další dílčí kritéria, jako např. výpočetní nároky, charakter rozložení dat, apod. Obecně nelze doporučit vhodný postup pro výběr optimální metriky ani pro úlohy určitých standardních typů.

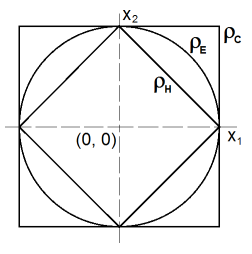
Je to metrika zřejmě s nejnázornější geometrickou interpretací. Geometrickým místem bodů s toutéž Euklidovou vzdáleností od daného bodu je koule (ve dvourozměrném prostoru kruh – viz Obr.1). Kvadrát rozdílů souřadnic znamená, že metrika klade větší důraz na větší rozdíly mezi souřadnicemi než v lineárním případě (což je třeba v každém konkrétním případě posoudit, zda je to stav žádoucí či nežádoucí). Pokud bychom počítali vzdálenost podle vztahu (12), ovšem bez použití odmocniny, tzv. kvadratická Euklidova metrika, pak je výpočet určitě méně náročný (není potřeba pracně odmocňovat), ale vztah nesplňuje trojúhelníkovou nerovnost. Vypočtené hodnoty lze považovat za míry nepodobnosti, ale výpočetní vztah není pravou metrikou. Kvadratickou euklidovskou vzdálenost lze tedy používat tehdy, kdy je rozhodující relativní porovnávání dvou hodnot (což například klasifikace podle minimální vzdálenosti je), nikoliv absolutní hodnoty jako takové.

Příklad 3.1

Určete hodnoty euklidovské vzdálenosti a kvadratické euklidovské vzdálenosti pro dvourozměrné body  = (0,0),  = (5,0) a  = (6,2).

Řešení:

Euklidovská vzdálenost:

Kvadratická euklidovská vzdálenost:

Zatímco pro libovolné dvě hodnoty Euklidovy vzdálenosti platí, že jejich součet je větší než zbývající hodnota, v případě kvadratické Euklidovy vzdálenosti je  není větší nebo rovno než – tedy neplatí trojúhelníková nerovnost.   

(13)

Tato metrika je také někdy nazývána manhattanská metrika, nebo v angličtině city-block metrika, resp. taxi driver metrika, protože svým výpočtem ve dvourozměrném prostoru navozuje představu vzdálenosti, kterou urazí automobil jedoucí z jednoho místa do druhého v pravoúhle zastavěném městském prostředí.

Hammingova metrika je vytvořena linearizací Euklidovy metriky, což má za následek jednak snížení významu členů s větším rozdílem mezi dílčími souřadnicemi obou vektorů, jednak snížení výpočetní pracnosti vůči Euklidově metrice. Absolutní hodnota je nezbytná pro zachování kladné výsledné hodnoty vzdálenosti. Geometrickým místem bodů s toutéž Hammingovou vzdáleností od počátku v dvourozměrném prostoru je čtverec uvnitř Euklidovy kružnice (viz Obr.1). Jak posléze uvidíme, Hammingova metrika má použití i při posuzování vzdáleností dvou binárních vektorů. Uplatňuje se i při hodnocení podobnosti dvou objektů, příp. jevů pomocí asociačních koeficientů.

Příklad 3.2

Zdůvodněte geometrickou reprezentaci Hammingovy metriky podle Obr.1.

Skryté řešení:

Jednotlivé obrazce v Obr.1 reprezentují body s toutéž vzdáleností dle dané metriky od počátku dvourozměrného prostoru, tj. od bodu x₁ = (0,0). Pro Hammingovu metriku v tom případě platí  = |0 - x₂₁| + |0 - x₂₂| = |x₂₁| + |x₂₂|. Z požadavku na stejnou vzdálenost proto platí |x₂₁| + |x₂₂| = konst.  Z toho plyne, že při platnosti tohoto vztahu musí být přírůstek jedné souřadnice kompenzován stejným úbytkem souřadnice druhé.

Dále z uvedeného vztahu je |x₂₂| = konst. - |x₂₁|. V prvním kvadrantu tento vztah reprezentuje přímku se směrnicí -1 a s absolutním členem rovným hodnotě dané vzdálenosti.

Obdobně uvedené relace platí i pro souřadnice x₂₁ a x₂₂ ze zbylých tří kvadrantů.  

Zobecňuje Euklidovu nebo v podstatě i Hammingovu metriku. Místo druhé mocniny, příp. odmocniny, je použita mocnina i odmocnina obecná. To znamená, že zvyšuje váhu vlivu členů s větším rozdílem dílčích souřadnic obou obrazů. Čím větší mocnina, tím větší důraz na větší rozdíly mezi souřadnicemi.

Vysvětlení pojmu 3.4 Čebyševova metrika je definována vztahem

(15)

Je limitním případem Minkovského metriky, protože platí

Používá se ve výpočetně kriticky náročných případech, kdy je pracnost výpočtu dle euklidovsky orientovaných metrik nepřijatelná. Geometrickým místem bodů s toutéž čebyševovskou vzdáleností od daného bodu je krychle, tj. čtverec ve dvourozměrném prostoru (Obr.1). Prostor mezi kružnicí euklidovské metriky D_E a čtvercem Čebyševovy metriky r_C vyplňují křivky Minkovského metriky pro různé hodnoty parametru .
Pokud je potřeba použít „euklidovskou“ metriku, ale s nižší výpočetní náročností, používá se v první řadě Hammingova nebo Čebyševova metrika. Možným přiblížením může být také kombinace obou metrik.
Vzdálenost určenou podle Hammingovy metriky lze považovat za dolní odhad vzdálenosti podle Euklidovy metriky a vzdálenost podle Čebyševovy metriky za její horní odhad.
Všechny uvedené metriky mají mnohé společné nevýhody. Jednak to, že je fyzikálně nesmyslné vytvářet součet rozdílů veličin s různým fyzikálním rozměrem, jednak to, že jsou-li do výsledné vzdálenosti začleněny veličiny se stejnými vahami, zvyšuje to vliv korelovaných veličin na celkový výsledek.
Tyto nevýhody mohou být odstraněny vhodnou transformací proměnných. Vliv různých fyzikálních veličin lze odstranit vztažením jejich hodnot k nějakému vyrovnávacímu faktoru, např. střední hodnotě , směrodatné odchylce , normě daného vektoru definované pro vektor x = (x₁, x₂, …, x_n) jako

rozpětí , resp. standardizací podle vztahu (někdy také nazývaného z-skóre)

Norma podle vztahu (17) v podstatě odpovídá Euklidově vzdálenosti vektoru od počátku souřadnicové soustavy.

Můžeme také buď čistě subjektivně, nebo lépe na základě nějaké objektivní apriorní informace přiřadit každé proměnné koeficient udávající její váhu při výpočtu vzdálenosti. Např. vztah pro Minkovského metriku se váhováním mění na

Transformaci pomocí váhových koeficientů lze vyjádřit maticovým zápisem

kde koeficienty transformační matice C jsou dány

S takovým vyjádřením transformace souřadnic je váhovaná Euklidova metrika pro sloupcové vektory definována vztahem

(22)

Příklad 3.3

Jaká by byla definice metriky D_WE(x₁,x₂) pro řádkové vektory?

Skryté řešení:

Pokud jsou složky transformovaného vektoru dány lineární kombinací více složek původního obrazu, není ani matice , ani matice  čistě diagonální. Použijeme-li místo matice inverzní kovarianční (disperzní) matici , je vztah (22) definičním vztahem tzv. Mahalanobisovy metriky

Kovarianční matice dvou sloupcových vektorů x = (x₁, …, x_m)^T a y = (y₁, …, y_n)^T je určena podle vztahu

Přestože použití kovarianční matice je pro Mahalanobisovu metriku naprosto dominantní, lze nalézt definice této metriky i s korelační maticí . V tomto případě je to opět situace, kdy je potřeba posoudit, zda je pro řešenou úlohu více informace v datech obsahujících i jejich střední hodnotu či zda střední hodnota pouze překrývá důležitou informaci obsaženou ve variabilitě dat.

Využívá-li výpočet vzdálenosti hodnot proměnných vztažených vůči rozdílům maximální a minimální hodnoty dané proměnné, pak na příklad Hammingova normovaná metrika je v tomto případě definovaná vztahem

kde max x_i a min x_i jsou maximální a minimální hodnoty dané souřadnice. Pro rozšíření intervalu, ve kterém se hodnoty vzdálenosti vyskytují, existuje i její logaritmická varianta definovaná jako

Ve všech těchto případech je třeba pečlivě zvážit, zda transformací dat nepřicházíme o významnou část informace, potřebné při navazujícím zpracování dat. Např. při použití Mahalanobisovy metriky, tak i při použití proměnných vztažených ke směrodatné odchylce, je potlačen vliv rozptylů proměnných na výslednou hodnotu vzdálenosti, což může mít na jedné straně příznivý, na druhé i nepříznivý vliv na získané výsledky a jejich interpretaci. Je potřeba si i uvědomit, že hodnota např. Mahalanobisovy metriky nebo normované Hammingovy metriky D_NHnx definované vztahem (25), příp. i metriky D_G, nezávisí pouze na poloze vektorů x₁ a x₂, nýbrž i na vlastnostech prostoru vektorů . To znamená, že nabývá-li na příklad vzdálenost určená metrikou  hodnoty  v prostoru a hodnoty  v prostoru , pak obecně .

Příklad 3.4

Mějme dva třírozměrné vektory x₁ = (0,1,2) a x₂ = (4,3,2).  Určete jejich vzdálenosti podle Hammingovy, Euklidovy a Čebyševovy metriky a dále vzdálenosti podle metriky (3.15), když zadané vektory patří

1. do prostoru s maximálními a minimálními hodnotami x_max = (10, 12, 13) a x_min = (0; 0,5; 1);
2. do prostoru s maximálními a minimálními hodnotami x‘_max = (20, 22, 23) a x‘_min = (-10; -9,5; -9);

Řešení:

Za předpokladu neváhovaných metrik je , a .

a)    v prostoru , který obsahuje vektory s maximálními hodnotami jednotlivých proměnných x_max = (10; 12; 13) a minimálními hodnotami souřadnic x_min = (0; 0,5; 1) je  d_G(x₁,x₂) = 0,0922.

b)    v prostoru s maximálními hodnotami proměnných x´_max = (20; 22; 23) a minimálními hodnotami x´_max = (-10; -9,5; -9) je d´_G(x₁,x₂) = 0,0295.          

V literatuře lze najít i verzi bez absolutních hodnot ve jmenovateli (tak, jak byl vzorec původně navržen), samozřejmě s dovětkem, že vztah je vhodný pouze pro kladné hodnoty proměnných.

Jednotlivé zlomky jsou z intervalu , celkový součet ale může být větší než 1. Je-li hodnota jedné souřadnice nulová, je dílčí zlomek roven jedné bez ohledu na druhou hodnotu. Jedničce se rovná dílčí zlomek i v případě, kdy obě souřadnice mají tutéž hodnotu, ale s opačným znaménkem. Jsou-li hodnoty obou proměnných ve zlomku nulové, pak předpokládáme, že i hodnota zlomku je nulová (někdy se z praktických výpočetních důvodů nahrazují nulové hodnoty velmi malými hodnotami – menšími než jsou nejmenší možné naměřené hodnoty). Canberrská metrika je velice citlivá na malé změny souřadnic, pokud se oba vektory nacházejí v blízkosti počátku souřadnicové soustavy. Naopak je méně citlivá na změny hodnot souřadnic, pokud jsou tyto hodnoty velké.

Příklad 3.5

Jaká je Hammingova a canberrská vzdálenost v obou případech a jaká je relativní změna vzdáleností vyvolaná uvedenou modifikací, pokud:

1. Jsou dány dva vektory x₁ = (0,001; 0,001) a x₂ = (0,01; 0,01) a předpokládejme, že souřadnice prvního z vektorů se změní na x₁´ = (0,002; 0,001).
2. Jsou dány dva vektory x₁ = (1000; 1000) a x₂ = (100; 100) a předpokládejme, že dojde ke změně první souřadnice vektoru x₁ na x´₁ = (1002; 1000).

Řešení:

d_H(x₁,x₂) = |0,001-0,01| + |0,001-0,01| = 0,009 + 0,009 = 0,018;

d_H(x´₁,x₂) = |0,002-0,01| + |0,001-0,01| = 0,008 + 0,009 = 0,017;

;

.

Relativní změny vzdáleností, určující citlivost té které metriky, které jsou způsobeny změnou hodnoty první souřadnice, jsou

.

Ze získaných výsledků je zřejmé, že relativní změna vzdáleností je v případě canberrské metriky pro toto zadání o poznání větší.

b)

d_H(x₁,x₂) = |1000-100| + |1000-100| = 900 + 900 = 1800;

d_H(x´₁,x₂) = |1002-100| + |1000-100| = 902 + 900 = 1802;

;

.

Relativní změny vzdáleností způsobených změnou hodnoty první souřadnice pak v tomto případě jsou

.

Jak je zřejmé, citlivost canberrské metriky je v tomto případě řádově menší.       

Kromě uvedených metrik s poměrně obecným použitím existuje řada dalších způsobů výpočtu nepodobnosti dvou vektorů odvozených pro speciální účely. Z nichž uveďme alespoň tzv. nelineární metriku definovanou vztahem

kde T je prahová hodnota a H je nějaká konstanta. I když existují doporučení, jak volit obě hodnoty na základě statistických vlastností vektorového prostoru, výhodnější se zdá volit obě konstanty na základě expertní analýzy řešeného problému. I když ve vztahu (28) je použita jako základní Euklidova metrika, teoreticky nic nebrání použití jakékoliv jiné metriky vzdálenosti.