Bayesův klasifikátor – kritérium maximální aposteriorní pravděpodobnosti

Kritérium maximální aposteriorní pravděpodobnosti je založeno na výpočtu aposteriorní podmíněné pravděpodobnosti zatřídění objektu  do třídy , jež se značí jako . Při výpočtu vycházíme z Bayesova vzorce:  

(3)

kde  je podmíněná hustota pravděpodobnosti výskytu objektu  ve třídě ;  je apriorní pravděpodobnost třídy  a  je celková hustota pravděpodobnosti rozložení objektu  v celém prostoru. Podmíněnou hustotu pravděpodobnosti  můžeme vypočítat na základě parametrického odhadu pomocí statistických rozdělení, nejčastěji vícerozměrného normálního rozdělení (ukázka v příkladu ), nebo pomocí Parzenových okének, což je metoda jádrového vyhlazování, či histogramu.

Jak již bylo zmíněno v předchozí podkapitole, pomocí diskriminačních funkcí můžeme vypočítat hranici mezi jednotlivými třídami. Pro hranici je rozdíl diskriminačních funkcí roven 0, tedy:

(4)

z čehož získáváme kritérium maximální aposteriorní pravděpodobnosti ve tvaru:

(5)

Podle tohoto kritéria tedy zatřídíme objekt x do třídy, jejíž pravděpodobnost je při výskytu objektu x větší. Konkrétně:

• když  → zařazení x do třídy
• když  → zařazení x do třídy

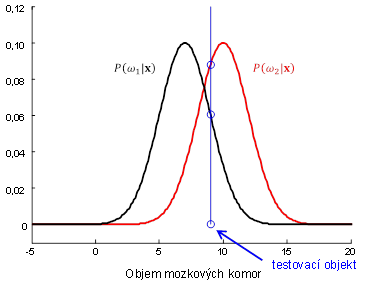
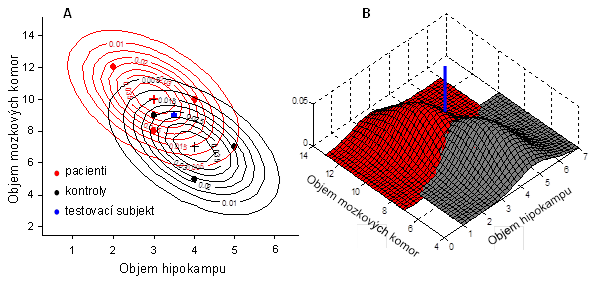
Názorná ilustrace je uvedena na Obr. 5 a Obr. 6 pro klasifikaci podle jedné respektive dvou proměnných. Testovací objekt v obou případech zařadíme do třídy , protože aposteriorní pravděpodobnost zařazení objektu x do třídy je větší než aposteriorní pravděpodobnost zařazení objektu x do třídy .