Verhulstův model růstu populace

Na Malthusovy úvahy reagoval v roce 1838 Pierre Francois Verhulst revizí Malhusova modelu, kdy specifickou míru růstu populace uvažoval klesající vzhledem k velikosti populace. Jde o model, ve kterém je zahrnuta tzv. vnitrodruhová konkurence, populace musí bojovat o omezené zdroje potravy, specifická míra růstu populace tedy klesá s velikostí populace. Verhust uvažoval tu nejjednodušší klesající funkci, tedy funkci lineární:

(2)

Kladný koeficient se nazývá kapacita prostředí, je vidět, že pokud velikost populace dosáhne kapacity prostředí, přírůstek populace bude nulový, je to tedy horní hranice velikosti populace, kterou je prostředí schopno uživit. Budeme předpokládat, že specifická míra růstu je kladná.

Nejprve budeme rovnici Základní modely populační dynamiky (2) studovat kvalitativními metodami. Rovnice má dva rovnovážné body: a přičemž pravá strana rovnice je kvadratická funkce vzhledem k (jejím grafem je konkávní parabola), která nabývá kladných hodnot v intervalu a vně tohoto intervalu nabývá hodnot záporných. Odtud je zřejmé, že rovnováha  je nestabilní a  je stabilní, dokonce asymptoticky. Velikost populace bude tedy směřovat ke kapacitě prostředí

Rovnici  Základní modely populační dynamiky (2) můžeme studovat také kvantitativně, tj. můžeme nalézt její obecné řešení, protože jde o rovnici separovatelnou. Jejím řešením je

Příklad. Nalezneme průběh funkce pro a Je zřejmé, že pro všechna a

funkce je tedy rostoucí, ohraničená limitami

a

To jsou rovnovážné body, které jsou -limitní a -limitní množinou uvedeného řešení. Protože

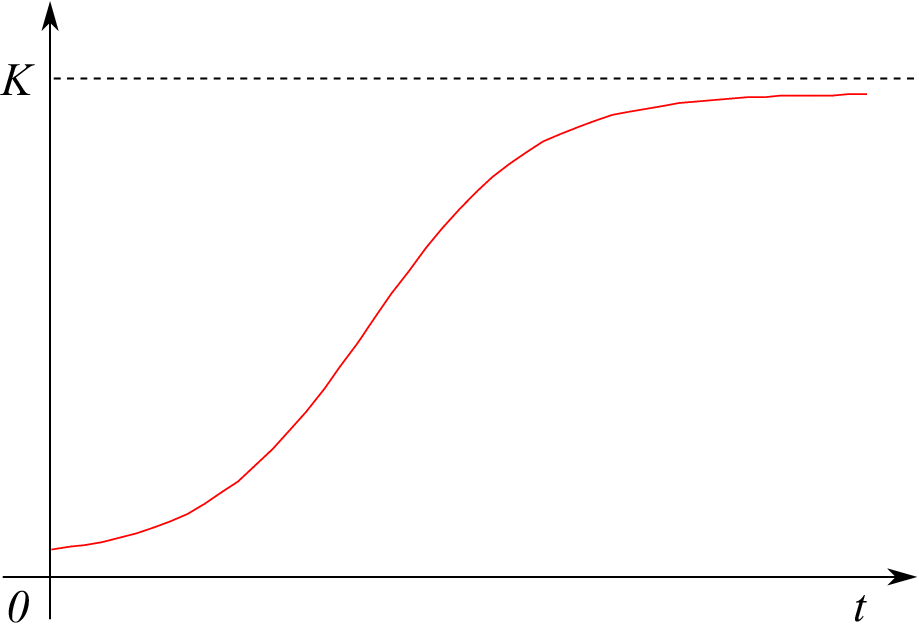
je inflexním bodem řešení bod v před tímto bodem je funkce konvexní a za ním konkávní. Hodnota Graf řešení ukazuje následující obrázek, říká se mu logistická křivka.