Model SIRS

Oproti modelu SIR v modelu SIRS předpokládáme, že uzdravení jedinci mohou znovu onemocnět. Vztahy mezi třídami populace jsou uvedeny v tabulce Epidemiologické modely 1. Stejně jako v modelu SIR budeme předpokládat, že velikost populace je neměnná. Podle rozdělení v  Modelování rychlostí přechodu můžeme za uvedených předpokladů získat tři základní modely SIRS:

Model SIR, kdy incidence roste lineárně s velikostí populace:

(7)

Model SIR s konstantní incidencí:

(8)

Model SIR s asymptoticky omezenou incidencí:

(9)

kde a jsou parametry. reprezentují okamžitý počet náchylných, infekčních a imunních jedinců v čase, přitom platí 

Počáteční podmínky všech modelů budou

(10)

Příklad. Uvažujeme systém Epidemiologické modely (7), Epidemiologické modely (10). Substitucí dostáváme dvojrozměrný model

(11)

s uvedenými počátečními podmínkami. Provedeme kvalitativní analýzu systému Epidemiologické modely (11). Rovnovážné body jsou  a Aby epidemie vypukla, musí tedy  odtud V případě lineární incidence je tedy reprodukční číslo závislé na velikosti populace Budeme tedy předpokládat nadále splnění této podmínky. Jacobiho variační matice  systému je

Pro bod  tedy platí

a vlastní čísla této matice jsou a bod  je tedy sedlo. Pro bod  platí

Stopa matice je záporná a determinant je kladný, proto má matice vlastní čísla se zápornou reálnou částí a bod  je stabilní uzel nebo ohnisko.

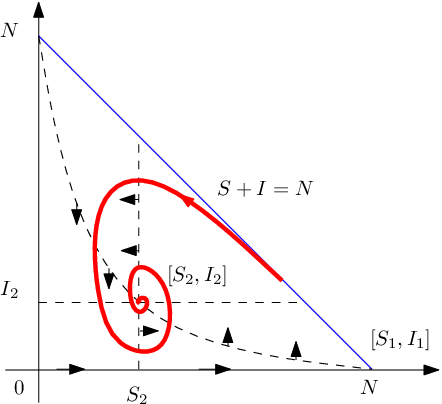
Fázový portrét systému Epidemiologické modely (11) ukazuje následující obrázek:

Obr. 3. Model průběhu epidemie SIRS

Epidemie má typický průběh, nejprve se počet infikovaných zvyšuje, poté se sníží na stabilní hladinu v případě ohniska je to oscilující konvergence.