Přibližné řešení úlohy Biochemické modely (10), Biochemické modely (11)

Charakteristickým rysem reakcí enzymu se substrátem je to, že koncentrace enzymu je výrazně menší, než koncentrace substrátu, To vzhledem k Biochemické modely (9) znamená, že

parametr je „skoro nula“. Také můžeme říci, že pravá strana druhé rovnice systému Biochemické modely (10) je „skoro nekonečno“, nebo že pravá strana první rovnice tohoto systému je zanedbatelně malá ve srovnání s pravou stranou druhé rovnice. Veličina  se mění „nesrovnatelně pomaleji“, než veličina  takže veličina je vzhledem k „skoro konstantní“. Z těchto důvodů budeme ve druhé z rovnic systému Biochemické modely (10) považovat za konstantní parametr a tuto rovnici vyřešíme. Jedná se o rovnici se separovanými proměnnými, takže její řešení splňující druhou podmínku z dvojice Biochemické modely (11), tj. podmínku dostaneme ve tvaru

(12)

Platí pro ně

„Rychle se měnící“ proměnná veličina (funkce) se tedy „velice rychle“ ustálí na hodnotě Ovšem hodnota se také mění, i když „pomalu“. Tato změna je popsána první rovnicí systému Biochemické modely (10). V ní můžeme proměnou považovat  za parametr rovný ustálené hodnotě  S využitím počáteční podmínky Biochemické modely (11) tak dostaneme počáteční úlohu

Řešení této úlohy, které je „trochu jiné“ než řešení původní úlohy Biochemické modely (10), Biochemické modely (11) a proto ho označíme symbolem je implicitně dáno rovností

(13)

Takto definovanou funkci můžeme považovat za první složku přibližného řešení úlohy Biochemické modely (10), Biochemické modely (11). Její druhou složku vyjádříme jako

(14)

tato funkce však nesplňuje druhou z počátečních podmínek Biochemické modely (11).

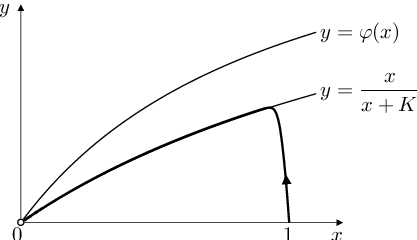
Obr. 5. Nulkliny systému Biochemické modely (10) a jeho trajektorie s počáteční podmínkou Biochemické modely (11) a hodnotou parametru

Funkce definované vztahy Biochemické modely (13) a Biochemické modely (14) se nazývá pseudo- nebo quasi-stacionární aproximace řešení úlohy Biochemické modely (10), Biochemické modely (11). V mnoha aplikacích je tato aproximace dostatečně přesná. Na obrázku Biochemické modely 5 je trajektorie řešení úlohy Biochemické modely (10), Biochemické modely (11) s hodnotou parametru  vidíme, že trajektorie řešení s „malou“ hodnotou parametru skutečně od jistého bodu téměř splývá s -nulklinou, tj. s funkcí

Řešení úlohy Biochemické modely (10), Biochemické modely (11) si tedy lze představit tak, že v „kratičkém časovém intervalu“ od začátku reakce se veličina (relativní množství substrátu) „nestačí změnit“, takže má stále počáteční hodnotu 1. V tomto „kratičkém čase“ veličina (relativní množství komplexu vzhledem k množství enzymu) rychle dosáhne své quasi-stacionární hodnoty. Tento „rychlý nárůst“ je popsán rovností Biochemické modely (12) do níž je dosazeno quasi-stacionární hodnota je tedy Dále se veličiny a vyvíjejí tak, jak je popsáno rovnostmi Biochemické modely (13) a Biochemické modely (14).

Ještě můžeme specifikovat délku zmíněného „kratičkého časového intervalu“ pro dosažení quasi-stacionárního stavu. Předpokládejme, že jsme schopni měřit koncentrace s relativní přesností Pak čas za nějž veličina naroste do quasi-stacionární hodnoty  je přibližně dána přibližnou rovnicí

tedy

(15)

Popsanou aproximaci řešení lze získat i jiným způsobem méně se odvolávajícím na intuici: řešení úlohy Biochemické modely (10), Biochemické modely (11) budeme hledat ve tvaru Taylorových řad v proměnné Předpokládejme tedy, že řešení úlohy Biochemické modely (10), Biochemické modely (11) je tvaru

Za předpokladu, že tyto řady, chápané jako řady funkcí proměnné konvergují stejnoměrně (k tomu při stačí, aby všechny funkce byly ohraničené stejnou konstantou), platí

a současně

Porovnáním koeficientů u stejných mocnin získáme nekonečný systém rovnic

Z první dvojice rovnic dostaneme

tedy quasi-stacionární aproximaci řešení Biochemické modely (13), Biochemické modely (14). V tomto případě však tato aproximace závisí na jedné integrační konstantě a ta závisí na počátečních podmínkách. Počáteční podmínky Biochemické modely (11) lze zapsat ve tvaru

takže z věty o jednoznačnosti Taylorových řad plyne

První z těchto podmínek lze splnit volbou stejně jako v Biochemické modely (13), ale druhou z nich splnit nelze. Odtud plyne, že alespoň jedna ze složek řešení úlohy Biochemické modely (10), Biochemické modely (11) nemůže být analytickou funkcí parametru

Aby bylo možné splnit počáteční podmínky, je třeba v pravém okolí bodu   hledat řešení úlohy Biochemické modely (10), Biochemické modely (11) jiným způsobem. Zavedeme novou nezávisle proměnnou

(16)

Pro je takže změnou časového měřítka Biochemické modely (16) „natáhneme malé okolí“ na „velice dlouhou dobu“. Substitucí Biochemické modely (16) se úloha Biochemické modely (10), Biochemické modely (11) transformuje na úlohu

(17)

(18)

Kvalitativní analýza úlohy Biochemické modely (17), Biochemické modely (11) dá stejné výsledky jako v ??.

Řešení úlohy Biochemické modely (17), Biochemické modely (18) budeme opět hledat ve tvaru Taylorových řad v proměnné tj. ve tvaru

Pak je

a současně

Z počátečních podmínek Biochemické modely (18) dostaneme

Nulté aproximace řešení úlohy Biochemické modely (17), Biochemické modely (11) jsou řešením počáteční úlohy

takže

Vrátíme se k původní nezávisle proměnné a dostaneme novou aproximaci řešení úlohy Biochemické modely (10), Biochemické modely (11) ve tvaru

(19)

tyto funkce splňují počáteční podmínky Biochemické modely (11).

Řešení úlohy Biochemické modely (10), Biochemické modely (11) lze v okolí bodu tj. na intervalu pro vhodné malé kladné číslo aproximovat funkcemi Biochemické modely (19). Tato část řešení úlohy se nazývá singulární nebo vnitřní řešení. Na intervalu lze použít quasi-stacionární aproximaci Biochemické modely (13), Biochemické modely (14); tato část řešení úlohy se nazývá nesingulární nebo vnější řešení.

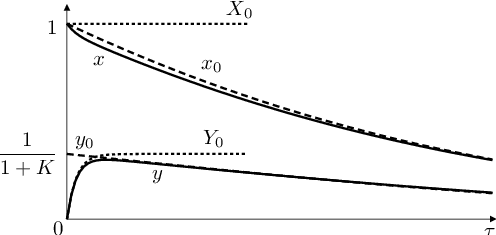
Na obr. Biochemické modely 6 je znázorněno přibližné a přesné řešení úlohy Biochemické modely (10), Biochemické modely (11) s parametrem vidíme, že již v tomto případě je přibližné řešení dosti blízké přesnému. Navíc, první složka řešení, tj. funkce je i v pravém okolí nuly přesněji aproximována vnějším řešením než vitřním.

Obr. 6. Řešení úlohy Biochemické modely (10), Biochemické modely (11) s parametrem Plná čára - přesné řešení, čárkovaná čára - vnější řešení, tečkovaná čára - vnitřní řešení.

Ještě odhadneme parametr - časový okamžik, od něhož vnější řešení lépe než vnitřní aproximuje druhou složku řešení úlohy Biochemické modely (10), Biochemické modely (11). Je to taková hodnota nezávisle proměnné, v níž mají funkce a stejnou hodnotu, Takové číslo  existuje podle Bolzanovy věty, neboť

Můžeme tedy řešit soustavu rovnic

Pak je

To znamená, že řešení druhé z rovnic, tj. rovnice leží v intervalu a funkce je na tomto intervalu rostoucí. Odtud dále plyne, že existuje konstanta taková, že pro řešení druhé z rovnic platí

Z první rovnice nyní dostaneme

Tato nerovnost vyjadřuje, že hodnota je malá stejného řádu, jako tj. Tento odhad souhlasí s vyjádřením Biochemické modely (15).

Řešení původní úlohy Biochemické modely (6), Biochemické modely (7) můžeme nyní zapsat ve tvaru

přitom funkce je implicitně dána rovnicí Biochemické modely (13).