Richardsova rovnice

(4)

je jednoduchou modifikací Verhulstovy rovnice. Křivka řešení oproti logistické křivce závisí na dalším parametru který ovlivňuje umístění inflexního bodu, což je velkou výhodou pro reálné aplikace. Následující obrázek je převzat z článku  Hsieh YH (2008) Richards Model: A Simple Procedure for Real-time Prediction of outbreak Severity. In: Zhien Ma, Jianhong Wu, Yicang Zhou, editors. In Modeling and Dynamics of Infectious Diseases. Beijing: Higher Education Press. Series in Contemporary Applied Mathematics (CAM), Vol. 11, 2008.9. Modelována je populace infikovaných osob respirační epidemií SARS.

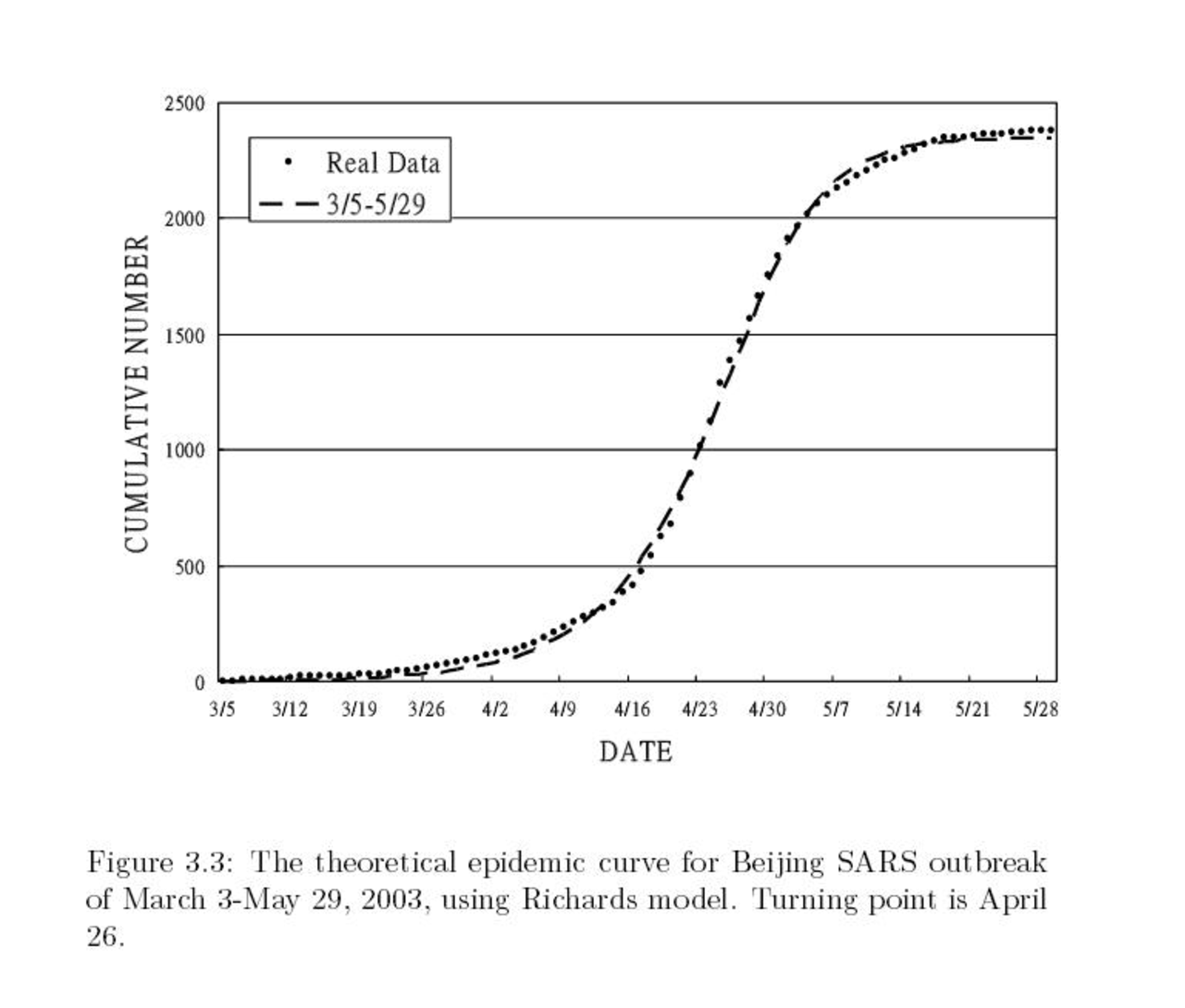Rovnici Základní modely populační dynamiky (4) lze převést na Verhulstovu pomocí vhodné substituce.

Tato rovnice je separovatelná lineární a je snadným cvičením nalézt její řešení. Zpětnou transformací pak dostáváme

Pokud uvažujeme počáteční podmínku pak musí platit

Řešením rovnice Základní modely populační dynamiky (4) s touto počáteční podmínkou je tedy

(5)