Globální vlastnosti řešení systému ODR

Věta o existenci úplného řešení

Věta 3.1. (o existenci úplného řešení). Nechť funkce je spojitá na otevřené množině Je-li řešení rovnice Obyčejné diferenciální rovnice (4), pak je toto řešení buď úplné, nebo existuje úplné řešení které je prodloužením řešení

Důkaz: Viz J. Kalas, M. Ráb: Obyčejné diferenciální rovnice. MU, Brno 2001, str. 73-76. Důkaz využívá věty Obecné vlastnosti obyčejných diferenciálních rovnic 2.7.

Definice 3.2. Buď Řekneme, že funkce je lokálně lipschitzovská v vzhledem k jestliže ke každému existuje okolí a číslo tak, že pro všechna platí

Věta o globální jednoznačnosti

Věta 3.3. (o globální jednoznačnosti). Nechť funkce  je spojitá a lokálně lipschitzovská v vzhledem k  a nechť funkce jsou dvě řešení rovnice Obyčejné diferenciální rovnice (4). Jestliže existuje takové, že pak pro všechna v nichž jsou řešení definována.

Důkaz. Připusťme, že existuje takové, že Označme

Funkce  jsou spojité (poněvadž jsou diferencovatelné).

Ukážeme, že

Připusťme, že Položme Pak

K existuje tak, že pro každé je a 

Poněvadž pro je platí pro nerovnost

což je spor s a tedy

Podle Obecné vlastnosti obyčejných diferenciálních rovnic 2.1 nyní existuje  takové, že pro je což je spor s předpokladem, že

Analogicky vyloučíme možnost existence takového, že 

Definice 3.4. Buď úplné řešení rovnice Obyčejné diferenciální rovnice (4) definované na intervalu kde

Řekneme, že je

• -limitní bod řešení  jestliže existuje posloupnost taková, že pro všechna  a 
• -limitní bod řešení  jestliže existuje posloupnost  taková, že  pro všechna   a 
•  limitní bod řešení  jestliže je  -limitním bodem nebo -limitním bodem.

Množina všech -limitních bodů řešení  se nazývá -limitní množina řešení  množina všech -limitních bodů řešení se nazývá -limitní množina řešení  množina všech limitních bodů řešení se nazývá limitní množina řešení 

Příklad. je úplné řešení rovnice definované na intervalu

Je-li pak je -limitním bodem tohoto řešení a -limitní body toto řešení nemá.

Je-li pak je -limitním bodem tohoto řešení a -limitní body toto řešení nemá.

Je-li pak je - i -limitním bodem tohoto řešení.

Příklad. je úplné řešení rovnice definované na intervalu Interval je -limitní množinou tohoto řešení.

Příklad.  je úplné řešení soustavy rovnic

 definované na intervalu Limitní množina tohoto řešení je

Věta 3.5. Nechť funkce je spojitá na otevřené množině a je úplné řešení rovnice Obyčejné diferenciální rovnice (4) definované na intervalu  Pak platí: 
, nebo , nebo každý -limitní bod řešení  leží na hranici
, nebo , nebo každý -limitní bod řešení  leží na hranici 

Důkaz. Buď  úplné řešení rovnice Obyčejné diferenciální rovnice (4) definované na intervalu   a buď jeho -limitní bod. Kdyby pak by existovalo okolí   bodu takové, že neboť je  otevřená. Podle Obecné vlastnosti obyčejných diferenciálních rovnic 2.7 by existovalo řešení rovnice Obyčejné diferenciální rovnice (4) s počáteční podmínkou definované na kde je vhodné (malé) číslo. Funkce

by byla řešením rovnice Obyčejné diferenciální rovnice (4), které by bylo prodloužením řešení  což by byl spor s úplností řešení 

Pro -limitní bod se důkaz provede analogicky s využitím „levostranné varianty“ věty Obecné vlastnosti obyčejných diferenciálních rovnic 2.7.

Důsledek 3.6. Nechť kde a a nechť vektorová funkce je spojitá. Pokud existuje spojitá funkce taková, že úplné řešení rovnice Obyčejné diferenciální rovnice (4) definované na  splňuje pro každé podmínku pak

Důsledek 3.7, Nechť  a funkce   je spojitá. Jestliže existuje takové, že pro každé platí pak každé úplné řešení rovnice Obyčejné diferenciální rovnice (4) je definováno pro všechna 

Důkaz. Buď  úplné řešení rovnice Obyčejné diferenciální rovnice (4). Podle Obecné vlastnosti obyčejných diferenciálních rovnic 1.1 je

Pro každé pro něž je definováno, platí

Tvrzení tedy plyne z Obecné vlastnosti obyčejných diferenciálních rovnic 3.6, položíme-li

Toto tvrzení umožňuje rozhodnout, zda lze každé řešení rovnice Obyčejné diferenciální rovnice (4) prodloužit do nekonečna, aniž bychom toto řešení znali.

Věta 3.8. Buď otevřená množina a nechť pro každé je vektorová funkce spojitá a Označme úplné řešení počátečního problému

Jestliže posloupnost funkcí konverguje k funkci stejnoměrně na každé kompaktní podmnožině posloupnost bodů konverguje k bodu a počáteční úloha

má jediné úplné řešení definované na intervalu pak posloupnost funkcí konverguje k funkci stejnoměrně na každém intervalu

Důkaz. Viz J. Kalas, M. Ráb: Obyčejné diferenciální rovnice. MU, Brno 2001, str. 80-82.

Matematické kyvadlo

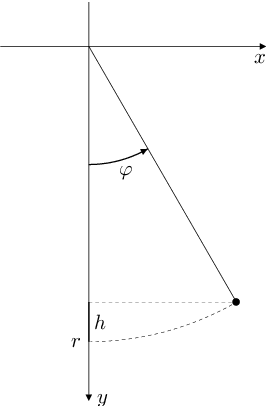
Příklad. Matematické kyvadlo je hmotný bod o hmotnosti zavěšený na nehmotném vlákně délky na který působí pouze gravitační síla. Lze ho realizovat jako kuličku zavěšenou na niti, přičemž průměr kuličky je zanedbatelný vzhledem k délce niti a hmotnost niti je zanedbatelná vzhledem k hmotnosti kuličky.   Zavedeme souřadný systém podle obrázku tak, že vodorovná osa směřuje zleva doprava a svislá osa směřuje shora dolů a kyvadlo je zavěšeno v počátku souřadnic. Označme výchylku kyvadla od rovnovážné polohy v čase Poloha hmotného bodu v čase je dána souřadnicemi

Obr. 3.1.

Vektor rychlosti hmotného bodu je derivací jeho polohy podle času, velikost rychlosti v čase je euklidovskou délkou tohoto vektoru, tj.

Výška hmotného bodu nad rovnovážnou polohou v čase je rovna

Podle zákona zachování energie je součet kinetické a potenciální energie hmotného bodu konstantní, tj.

přitom je gravitační konstanta. Do předchozí rovnosti dosadíme vypočítané a a dělíme ji konstantou Dostaneme

Tuto rovnost derivujeme podle času

a upravíme

Dostáváme tedy dvě diferenciální rovnice pro časově proměnnou výchylku kyvadla

(3)

Nechť na začátku procesu je výchylka hmotného bodu rovna úhlu a jeho rychlost, tj. změna výchylky, je nulová (kuličku vychýlíme a pustíme). Dostáváme tak počáteční podmínky

(4)

Řešení první z rovnic Obecné vlastnosti obyčejných diferenciálních rovnic (3) s počáteční podmínkou Obecné vlastnosti obyčejných diferenciálních rovnic (4) je konstantní funkce Toto řešení není fyzikálně realistické, neboť hmotný bod pod vlivem gravitační síly nemůže zůstat vychýlený z rovnovážné polohy a nepohybovat se.

Obr. 3.2.

Dosavadními úvahami dostáváme model pohybu matematického kyvadla jako počáteční úlohu pro obyčejnou diferenciální rovnici druhého řádu

 

kterou můžeme podle Existence a jednoznačnost řešení systému ODR přepsat jako počáteční úlohu pro systém dvou rovnic prvního řádu

(5)

Tuto počáteční úlohu neumíme vyřešit explicitně. Funkci sinus však můžeme vyjádřit jako stejnoměrně konvergentní Maclaurinovu řadu

Označme nyní

Pro   zavedeme vektorové funkce a body následujícími formulemi

Funkce  a body  splňují předpoklady věty Obecné vlastnosti obyčejných diferenciálních rovnic 3.8 s Úloha

(6)

je totožná s úlohou Obecné vlastnosti obyčejných diferenciálních rovnic (5). Poněvadž všechny parciální derivace

jsou ohraničené, je podle tvrzení Obecné vlastnosti obyčejných diferenciálních rovnic 2.4 úloha Obecné vlastnosti obyčejných diferenciálních rovnic (6) jednoznačně řešitelná. To znamená, že řešení úlohy Obecné vlastnosti obyčejných diferenciálních rovnic (5) je stejnoměrnou limitou řešení úloh

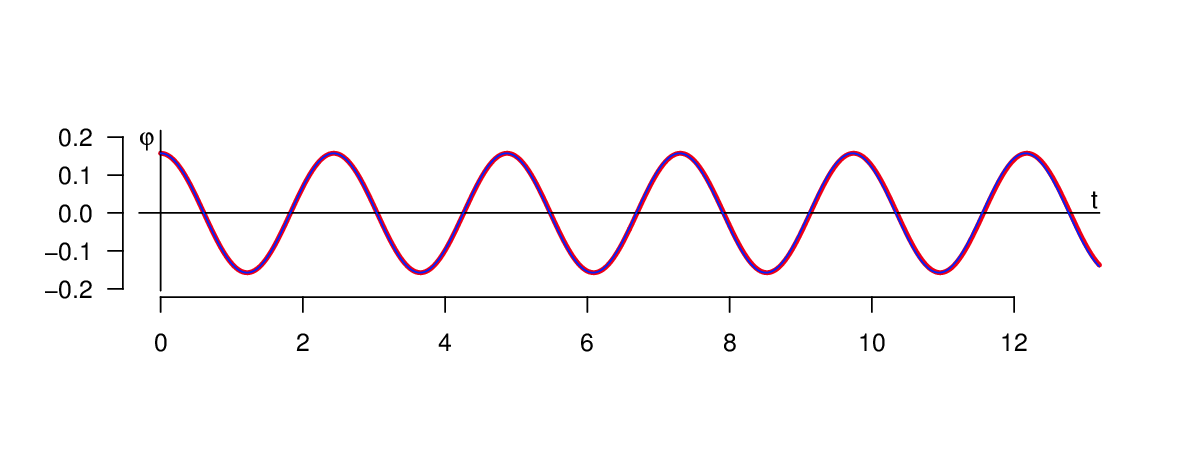
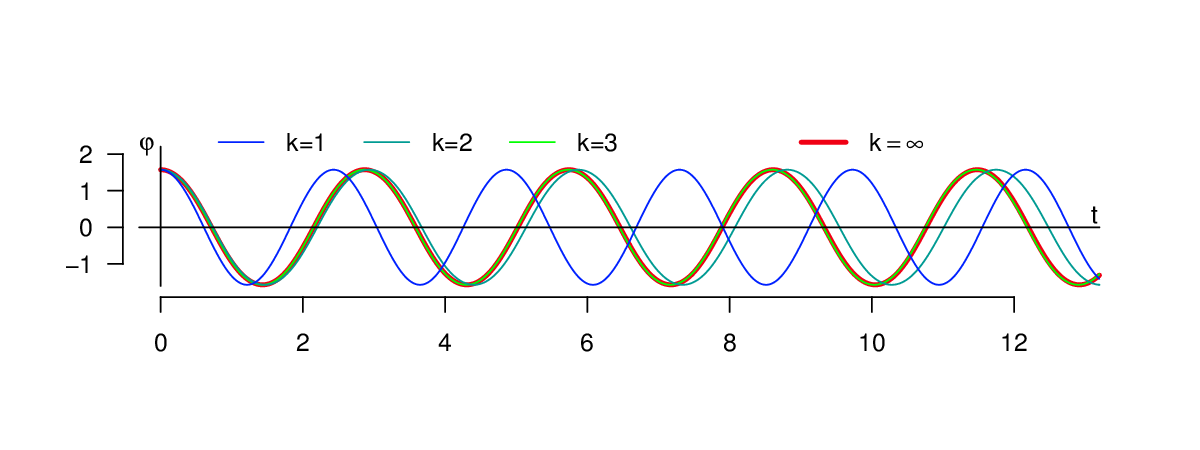
(7)

Na obrázku 2 je zobrazena první složka řešení (výchylka kyvadla ) několika těchto úloh; nahoře pro počáteční hodnotu dole pro Vidíme, že v případě malé počáteční výchylky již první člen posloupnosti dostatečně přesně aproximuje řešení úlohy Obecné vlastnosti obyčejných diferenciálních rovnic (5). V případě velké počáteční výchylky, dokonce maximální možné, je řešení úlohy Obecné vlastnosti obyčejných diferenciálních rovnic (5) dostatečně přesně aproximováno třetím členem posloupnosti řešení úloh Obecné vlastnosti obyčejných diferenciálních rovnic (7).

Malé kmity matematického kyvadla lze tedy modelovat systémem rovnic

který je ekvivalentní s rovnicí druhého řádu 

Věta o spojité závislosti řešení na počátečních podmínkách a parametrech

Věta 3.9. (o spojité závislosti řešení na počátečních podmínkách a parametrech). Buď otevřená množina v a nechť spojitá funkce je taková, že pro všechna splňující podmínku má počáteční problém

právě jedno úplné řešení Pak toto řešení, chápané jako zobrazení

je spojité.

Důkaz. Viz  J. Kalas, M. Ráb: Obyčejné diferenciální rovnice. MU, Brno 2001, str. 82-83.

Tato věta říká, že změní-li se málo funkce v rovnici Obyčejné diferenciální rovnice (4) a málo se změní počáteční podmínka Obyčejné diferenciální rovnice (5), pak se řešení nového - změněného - problému liší na konečném intervalu málo od řešení původního problému.