Obyčejná diferenciální rovnice prvního řádu

Převážně budeme pracovat s reálnými funkcemi jedné reálné proměnné, kterou označíme . Je-li , budeme psát 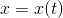 nebo . Obyčejnou derivaci funkce 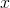 v bodě  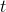(v čase 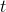) značíme  nebo jako podíl diferenciálů, tedy  Zápis  označuje derivaci funkce 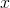 v obecném bodě. Můžeme tedy psát  a obecně pro 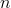-tou derivaci  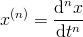 nebo stručně .

 

Příklad: Uveďme si nyní příklad, na kterém si jednotlivé pojmy představíme. Pěstujeme bylinky. To je reálný proces probíhající v čase. Reálná funkce  bude představovat množství biomasy v čase . Derivace   představuje okamžitý přírůstek, okamžitou změnu množství biomasy neboli rychlost růstu našich bylinek. Druhá derivace je změna této rychlosti.  Proč tomu tak je? 

 

Budeme nejprve předpokládat, že bylinky denně plynule rostou stále stejně rychle. Můžeme tedy uvažovat spojitý čas (v jednotkách dnů). Změna množství bylinek za jeden den je 

 

 

Pokud budeme předpokládat, že ani během dne se rychlost růstu nemění (to je jistě idealizace), pak za čas  bude přírůstek biomasy

 

 

Tedy i limitně platí

 

 

Derivace je tedy okamžitou rychlostí růstu neboli změnou množství  za nekonečně malý časový interval. Druhá derivace je analogicky okamžitá změna této rychlosti, okamžité zrychlení, akcelerace tohoto růstu. Pokud bylinky nebudou růst stále stejně rychle, bude rychlost jejich růstu nekonstantní funkcí času. Budeme-li například bylinky hnojit, můžeme tím zvyšovat rychlost jejich růstu, . Pokud je napadnou mšice, bude naopak , přestože bylinky i tak asi porostou.

 

Definice 1.1. Nechť 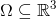je množina s neprázdným vnitřkem,   je funkce tří proměnných. Rovnice

Řešením této rovnice se rozumí diferencovatelná funkce , kde 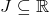 je interval, která splňuje

Uvedená rovnice se nazývá implicitní nebo nerozřešená vzhledem k derivaci. Pokud se podaří derivaci 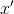 z rovnice

vyjádřit, dostaneme explicitní rovnici nebo rovnici rozřešenou vzhledem k derivaci.

 

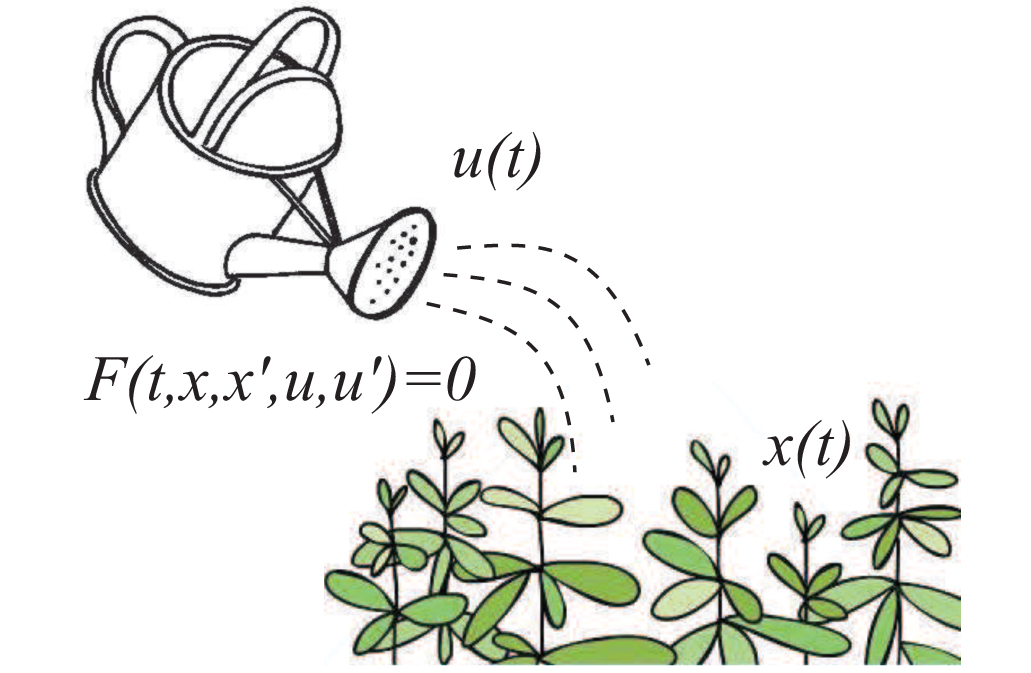
Poznámka 1.2. V teorii dynamických systémů (signálů) se velmi často používá jiné obecnější definice obyčejné diferenciální rovnice 1. řádu, kde funkce 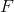 má ještě další dvě složky, tj. 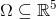. Rovnice

pak představuje diferenciální rovnici 1. řádu, kde 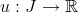  je funkce představující vstup a řešení  výstup dynamického systému. Řešení 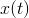 (výstup) obecně závisí na vstupní funkci .

Definice 1.3. Buď 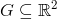 množina s neprázdným vnitřkem, . Rovnice

(1)

Řešením této rovnice se rozumí diferencovatelná funkce , kde 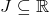 je interval, která splňuje

Definice 1.4.  Nechť 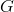,  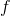mají stejný význam jako v definici Obyčejné diferenciální rovnice 1.3 a nechť  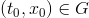je libovolný bod. Úloha najít řešení rovnice Obyčejné diferenciální rovnice (1), které splňuje podmínku

(2)

Příklad: Vraťme se k našim bylinkám. Když za jeden den vyrostou bylinky o 5%, můžeme růst bylinek modelovat diferenciální rovnicí  rozřešenou vzhledem k derivaci, kde čas  běží spojitě (v jednotkách dnů) a vystupuje skrze proměnnou biomasu. Rovnice, kde čas explicitně nevystupuje se nazývají autonomní. Pokud budeme bylinky každý den spotřebovávat, přičemž např. naše spotřeba bude narůstat každý den o 2 gramy, bude diferenciální rovnicí popisující množství bylinek rovnice

 

                                                                                                        

(3)

 

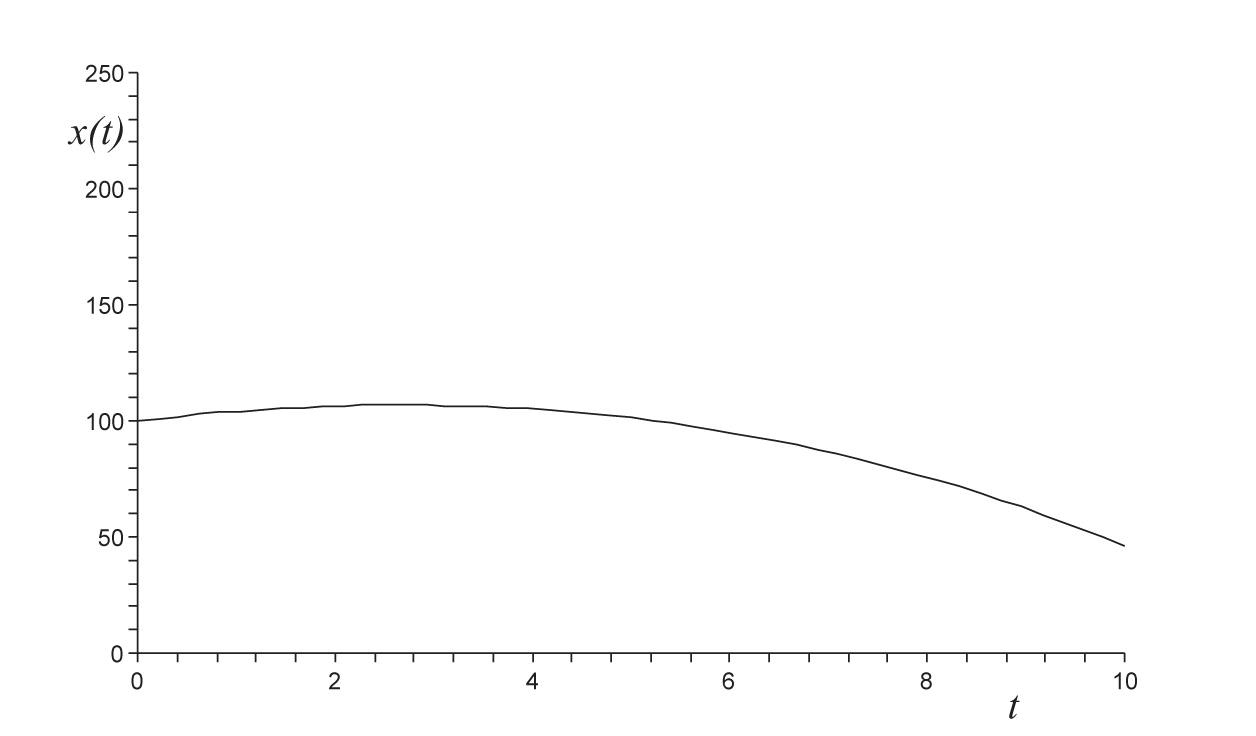
Pokud bychom na začátku měli 100g bylinek (jde tedy o počáteční podmínku ),  bude řešením funkce  (ověřte!) a grafem řešení bude

 

 

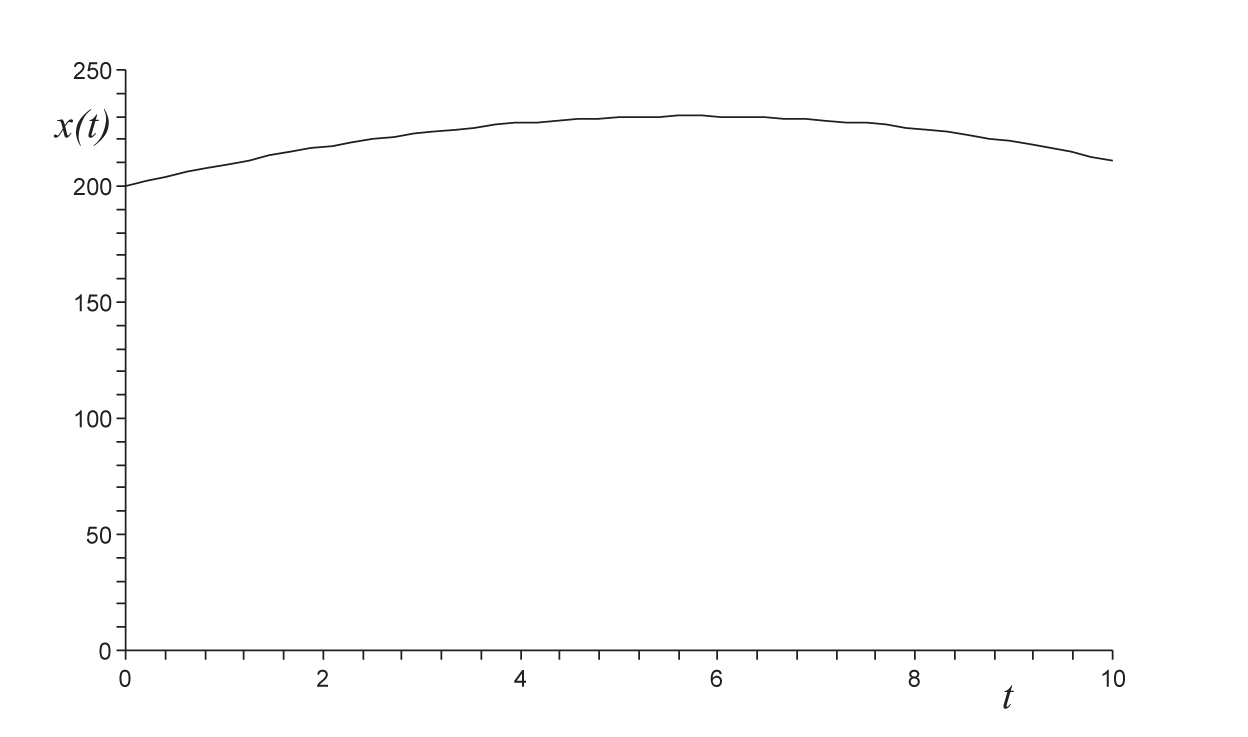
Pokud bychom na začátku měli 200g bylinek (jde tedy o počáteční podmínku ), bude řešením funkce  (ověřte!) a grafem řešení bude