Slovník | Vyhledávání | Mapa webu
 
Analýza a modelování dynamických biologických datSpojité deterministické modely I Elementární metody řešení Další metody řešení vybraných typů obyčejných diferenciálních rovnic Rovnice nerozřešená vzhledem k derivaci
Logo Matematická biologie

Rovnice nerozřešená vzhledem k derivaci

 
Rovnice nerozřešená vzhledem k derivaci
  (implicitní rovnice).
 
 
Zavedeme funkci 
 
 
1. Rovnice autonomní 
 
Rovnicí  může být implicitně zadána funkce . Rovnici  derivujeme podle proměnné :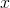
 

 

což je rovnice pro neznámou funkci 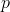 nezávisle proměnné  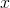rozřešená vzhledem k derivaci.
Je-li  řešením poslední rovnice, pak rovnice se separovanými proměnnými  je řešením původní
rovnice; její obecné řešení je tedy implicitně zadáno rovnicí
 
 
2. Rovnice nezávisející na neznámé funkci 
 
Rovnici  derivujeme podle proměnné :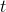

 

což je rovnice pro neznámou funkci  rozřešená vzhledem k derivaci. Je-li  řešením poslední rovnice, je funkce  obecným řešením dané rovnice.
 
3. Clairautova rovnice 
 
Rovnici  derivujeme podle proměnné :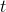       
 

 

Musí tedy být  nebo .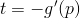 
 
Z  první rovnosti a dané rovnice dostaneme obecné řešení
 
 
kde  je libovolná konstanta; z druhé rovnice dostaneme parametrické vyjádření singulárního řešení
                 

 

kde 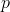 je parametr.
 
4. Lagrangeova rovnice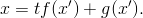 
 
Rovnici  derivujeme podle proměnné :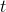
 

 

Má-li rovnice 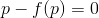 řešení , pak  je singulárním řešením dané rovnice. Konstantu 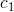 určíme dosazením do dané rovnice:
 
a poněvadž 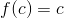, je . Singulární řešení Lagrangeovy rovnice tedy je
 
 
kde  je řešením rovnice  (je pevným bodem funkce ).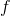 
 
Pro  dostaneme
 
 
což je lineární rovnice pro neznámou funkci 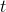nezávisle proměnné 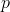. Označíme-li její řešení , pak
 
je parametrickým vyjádřením obecného řešení Lagrangeovy rovnice.
 

 

 
vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity