Homogenní lineární rovnice s konstantními koeficienty

(18)

Řešení hledáme ve tvaru Pak 

a tedy

(19)

Poněvadž pro všechna můžeme rovnici touto funkcí vykrátit. Dostaneme

(20)

Rovnice Lineární rovnice (19) se nazývá charakteristická rovnice lineární diferenciální rovnice Lineární rovnice (18).

Speciální případ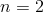 

Řešíme rovnici druhého řádu

(20)

kde jsou reálné parametry. Charakteristická rovnice této diferenciální rovnice

(21)

má kořeny

Rozlišíme tři možnosti:

(i)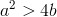 

V tomto případě má charakteristická rovnice Lineární rovnice (21) dva reálné různé kořeny Funkce

jsou řešením diferenciální rovnice Lineární rovnice (20). Wronskián těchto funkcí je

To znamená, že funkce tvoří fundamentální systém řešení rovnice Lineární rovnice (20).

(ii)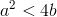 

Označme

 pak Charakteristická rovnice Lineární rovnice (21) má komplexně sdružené kořeny Komplexní funkce

jsou řešením diferenciální rovnice Lineární rovnice (20). Podle principu superpozice věta Lineární rovnice 2.1 jsou také reálné funkce

řešením této diferenciální rovnice. Jejich derivace jsou

takže pro jejich wronskián platí

Funkce   jsou lineárně nezávislé, tvoří tedy fundamentální systém řešení a obecné řešení rovnice Lineární rovnice (20) je

kde jsou konstanty. Pokud je řešení netriviální, je alespoň jedna z nich nenulová a platí

a proto existuje číslo takové, že

Označme nyní Obecné řešení rovnice Lineární rovnice (20) přepíšeme do tvaru

Poznamenejme, že v tomto tvaru řešení je zahrnuto i řešení triviální 

(iii)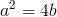 

V tomto případě je diferenciální rovnice tvaru

(22)

a její charakteristická rovnice má jeden dvojnásobný kořen Jedno řešení diferenciální rovnice Lineární rovnice (22) je tedy funkce

Spolu s rovnicí Lineární rovnice (22) uvažujme pomocnou rovnici

(23)

Její charakteristická rovnice

má dva reálné různé kořeny  Pomocná rovnice Lineární rovnice (23) má tedy podle výsledku (i) fundamentální systém řešení

Podle principu superpozice má lineární rovnice Lineární rovnice (23) také řešení

Poněvadž levá strana strana rovnice Lineární rovnice (22) je limitou levé strany pomocné rovnice Lineární rovnice (23) pro lze očekávat, že také funkce bude v limitě  řešením původní rovnice Lineární rovnice (22). S využitím de l'Hospitalova pravidla dostaneme

Ověříme, že funkce je skutečně řešením rovnice Lineární rovnice (22). Platí

takže

a funkce je řešením rovnice Lineární rovnice (22). Wronskián funkcí je

Funkce   jsou lineárně nezávislá řešení rovnice Lineární rovnice (22), tvoří tedy její fundamentální systém řešení.

Rovnice obecného řádu

Řešení rovnice Lineární rovnice (18) řádu je přímým zobecněním předchozího speciálního případu.

Lemma 6.1. Pokud je -násobný kořen charakteristické rovnice, pak funkce

jsou řešení rovnice Lineární rovnice (18).

Důkaz. Označme a pravou stranu charakteristické rovnice Lineární rovnice (19). Poněvadž je -násobný kořen charakteristické rovnice, platí

(24)

 

Funkce vyjádříme ve tvaru

dosadíme je do pravé strany rovnice Lineární rovnice (18) a upravíme s využitím Leibnizovy formule pro vyšší derivace součinu funkcí. Dostaneme

podle Lineární rovnice (24). Funkce tedy splňují rovnici Lineární rovnice (18).

Lemma 6.2. Nechť jsou všechny navzájem různé kořeny charakteristické rovnice Lineární rovnice (19), přičemž kořen je -násobný, Pak funkce

tvoří fundamentální systém řešení rovnice Lineární rovnice (18).

Důkaz. Každá z funkcí je řešením rovnice Lineární rovnice (18) podle lemma Lineární rovnice 6.1. Stačí tedy dokázat jejich lineární nezávislost, tj. ukázat, že jejich wronskián

je nenulový pro všechna . Připusťme, že existuje že Pak podle lemma Lineární rovnice 2.2 je pro všechna . Wronskián má lineárně závislé řádky a tedy existují konstanty mezi nimiž je alespoň jedna nenulová, takové že

pro všechna

Pro a -krát diferencovatelnou funkci nyní položíme

Pak je polynom stupně nejvýše Pro funkci a pro libovolné platí

Zejména pro  dostáváme 

To znamená, že je kořenem -té derivace polynomu pro každé tedy  je -násobným kořenem polynomu

Analogicky ukážeme, že  je -násobným kořenem polynomu pro všechna Polynom tedy musí být stupně alespoň a to je spor.

Lemma Lineární rovnice 6.2 umožňuje zkonstruovat fundamentální systém řešení lineární rovnice Lineární rovnice (18). Mezi jeho prvky však mohou být i komplexní funkce, neboť polynom na levé straně charakteristické rovnice Lineární rovnice (19) může mít komplexně sdružené kořeny. Popíšeme, jak komplexní funkce z fundamentálního systému nahradíme lineárně nezávislými reálnými funkcemi.

Nechť je -násobný komplexní kořen charakteristické rovnice Lineární rovnice (19). Pak také komplexně sdružené číslo  je -násobným kořenem charakteristické rovnice a ve fundamentálním systému řešení z lemma Lineární rovnice 6.2 jsou funkce

Bez újmy na obecnosti můžeme funkce z fundamentálního systému přečíslovat tak, že

Lemma 6.3. Nechť  je fundamentální systém řešení rovnice Lineární rovnice (18) popsaný předchozí konstrukcí. Položme

Pak funkce tvoří fundamentální systém řešení rovnice Lineární rovnice (18).

Důkaz. Funkce jsou řešením rovnice Lineární rovnice (18) podle principu superpozice Lineární rovnice 2.1. Ukážeme, že funkce  jsou lineárně nezávislé.

Položme

Pak

a pro wronskián funkcí  platí

Závěr

Každému reálnému -násobnému kořenu charakteristické rovnice Lineární rovnice (19) odpovídá řešení

diferenciální rovnice Lineární rovnice (18) a každé dvojici -násobných nereálných kořenů charakteristické rovnice Lineární rovnice (19) odpovídá reálných řešení

diferenciální rovnice Lineární rovnice (18). Množina řešení odpovídající všem kořenům charakteristické rovnice Lineární rovnice (19) tvoří fundamentální systém řešení homogenní lineární diferenciální rovnice -tého řádu s konstantními koeficienty Lineární rovnice (18).