Model SIR

Oproti modelu SI v modelu SIR předpokládáme, že uzdravení jedinci již získávají vůči dané nemoci imunitu (alespoň dočasnou), viz diagram v tabulce Epidemiologické modely 1. Stejně jako v modelu SI budeme předpokládat, že velikost populace je neměnná. Podle rozdělení v  Modelování rychlostí přechodu můžeme za uvedených předpokladů získat tři základní modely SIR:

Model SIR, kdy incidence roste lineárně s velikostí populace:

(3)

Model SIR s konstantní incidencí:

(4)

Model SIR s asymptoticky omezenou incidencí:

(5)

kde a jsou parametry uvedené v předchozí podkapitole. reprezentují okamžitý počet náchylných, infekčních a imunních jedinců v čase, přitom platí 

Počáteční podmínky všech modelů budou

(6)

Epidemiolog potřebuje odpovědi na následující otázky. Bude epidemie šířit a jak rychle?  Kdy dojde k vrcholu epidemie a jak dlouho epidemie potrvá? Kolik jedinců nakonec onemocní a kolik ne? Jak nejefektivněji předpokládané stavy snížit? Modelové řešení těchto problémů si ukážeme na modelu SIR Epidemiologické modely (4) s konstantní incidencí.

Příklad. Uvažujeme tedy systém Epidemiologické modely (4), Epidemiologické modely (6). Epidemie se začne šířit v okamžiku, kdy Protože

a na počátku je začne se epidemie šířit, pokud Zavádí se poměr který se označuje jako základní reprodukční číslo. Toto číslo vyjadřuje průměrný počet sekundárních infekcí vzniklých tím, že se jeden infikovaný jedinec dostane do plně náchylné populace, protože sekundární infekce jsou dány součinem průměrné doby trvání nemoci a počtu nakažených za jednotku času Pokud je infekce se bude šířit. Pro představu uvedeme odhady základních reprodukčních čísel pro některé nemoci:

Tab. 2. Odhady základních reprodukčních čísel

Systém Epidemiologické modely (4), Epidemiologické modely (6) budeme analyzovat kvalitativně. Rovnovážné stavy splňují    a Přitom Pro rovnovážný stav tedy nutně platí

Zřejmě všechny body této křivky jsou také rovnováhami. Nejde tedy o izolované hyperbolické rovnovážné body, nemůžeme proto použít metodu linearizace. Uvažujme ale takto: mimo rovnovážné body pro platí počet náchylných jedinců tedy klesá a můžeme označit Dále také tedy i má limitu pro Existuje tedy nutně i limita

a

Proto Epidemie má tedy takový průběh, že se nejprve počet infikovaných zvyšuje, ale poté musí klesnout limitně k nule. Navíc z první a třetí rovnice systému Epidemiologické modely (4) dostáváme pro počet náchylných jedinců

kde je konstantní. Pro řešení této rovnice (počet náchylných v závislosti na uzdravených) platí Pokud by tomu tak nebylo, tedy pokud by platilo pak také   a což je stav, který neopovídá našemu předpokladu počátečního vstupu infekčních osob do zdravé populace. I kdybychom tuto situaci uvažovali (plně infikovaná populace), je tento stav nestabilní, protože a počet uzdravených se rychle zvyšuje. Vždy jsou tedy v populaci jedinci, kteří nejsou infikovaní.

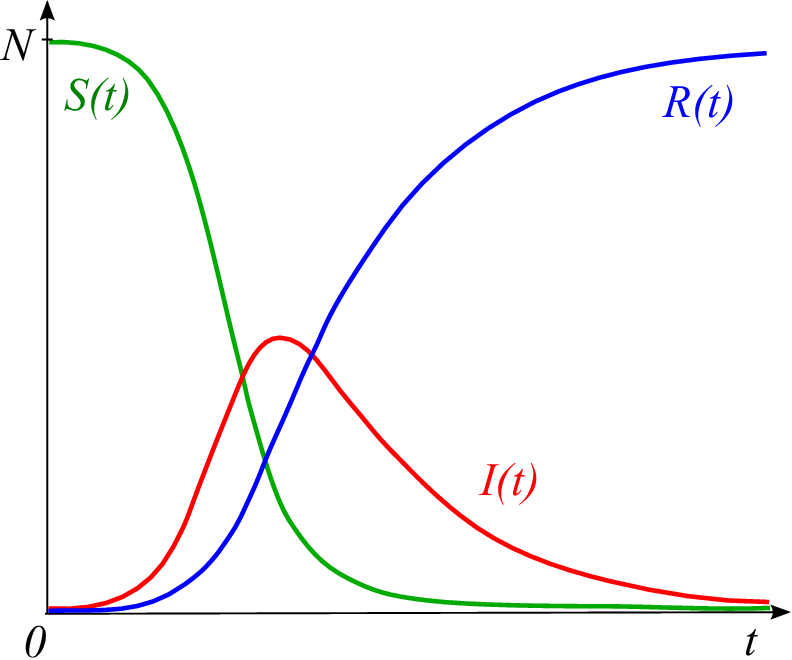
Průběh a ukazuje obrázek 

Počáteční rychlost růstu epidemie určuje

Čím větší je základní reprodukční číslo tím rychlejší nástup epidemie má. Na vrcholu epidemie platí proto Navíc

což je separovatelná rovnice, jejíž řešení je Uvažujeme-li tedy na počátku zdravou populaci, je pro a odtud dostáváme partikulární řešení tvaru  Na vrcholu epidemie je a počet infikovaných proto bude

Podobně bychom mohli pokračovat a vypočítat, kdy dojde k vrcholu epidemie, kolik nemocných celkem onemocní apod. Toto už necháme na čtenáři.

 

Úlohy k procvičení