Uvažujme chorobu, která trvá krátce,někteří pacienti na ni zemřou, jiní se uzdraví a získají vůči nákaze imunitu; typickým představitelem takové infekce byly neštovice. Budeme modelovat epidemii této choroby, tj. její šíření v nějaké kohortě. Kohortou rozumíme skupinu osob narozených ve stejnou dobu.

Zavedeme označení: počet osob zahrnutých do kohorty, jejich věk (tj. čas od počátku), resp. počet osob věku které neprodělaly, resp. prodělaly, chorobu. Při tomto označení je neboť novorozenci chorobu neprodělali, tj. Další symboly zavedeme na základě následujících předpokladů:

očet osob věku které zemřou z jiných příčin, než je uvažovaná infekce, je úměrná délce (krátkého) časového intervalu sledování a počtu nenakažených osob Konstantu úměrnosti - přirozenou úmrtnost ve věku - označíme
Počet osob věku které se nakazí uvažovanou chorobou je úměrná délce sledování a počtu osob, které dosud chorobu neprodělaly a jsou tedy citlivé na infekci. Koeficient úměrnosti - incidenci choroby ve věku - označíme
Počet nemocných osob věku které se uzdraví za časový interval je úměrný počtu infikovaných osob tohoto věku a délce intervalu Koeficient úměrnosti - index přežití choroby osobami věku - označíme

Úmrtnost lze interpretovat jako pravděpodobnost, že „zdravá“ osoba (tj. ta, která nemá uvažovanou chorobu) věku zemře během časového intervalu délky incidenci jako pravděpodobnost, že se „zdravá“ osoba věku která není imunní vůči uvažované chorobě, nakazí během časového intervalu délky ukazatel přežití jako pravděpodob-nost, že nakažená osoba věku se během časového intervalu délky uzdraví. Budeme předpokládat, že onemocnění a uzdravení jsou jevy nezávislé, tj. že pravděpodobnost, že osoba citlivá k infekci se během časového intervalu délky nakazí a uzdraví, je rovna Dále zavedeme letalitu choroby ve věku vztahem

lze ji interpretovat jako pravděpodobnost, že nemocná osoba věku během časového intervalu délky zemře. Proměnné

vyjadřují (klasickou) pravděpodobnost, že osoba se dožila věku a neprodělala, resp. prodělala, chorobu. Novorozenec určitě chorobu neprodělal, tedy platí

(31)

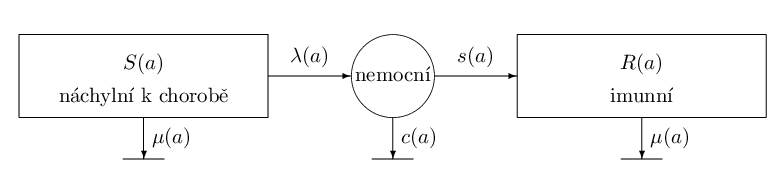
Obr. 7.4. Schéma vývoje kohorty ohrožené chorobou.

Vývoj kohorty, v níž probíhá choroba, lze schematicky znázornit obrázkem 4 a předpoklady vyjádřit ve tvaru rovností:

V první z uvedených rovností převedeme na levou stranu a ve druhé z nich rovnosti vydělíme výrazem a provedeme limitní přechod Pro zjednodušení modelu budeme předpokládat, že funkce a jsou diferencovatelné; takový předpoklad je v případě velké kohorty dostatečně realistický. Dostaneme tak systém neautonomních diferenciálních rovnic

(32)

jejich řešení splňuje počáteční podmínky Některé klasické úlohy (31).

První rovnice systému Některé klasické úlohy (32) je lineární homogenní rovnicí pro neznámou funkci Její řešení s počáteční podmínkou Některé klasické úlohy (31) je při označení

(33)

podle ref{elreslinrov} rovno

(34)

Toto vyjádření dosadíme do druhé rovnice systému Některé klasické úlohy (32) a dostaneme

což je lineární nehomogenní rovnice pro neznámou funkci Její řešení s počáteční podmínkou Některé klasické úlohy (31) je opět podle ref{elreslinrov} rovno

(35)

Dosud provedené úvahy a výpočty lze shrnout: Pravděpodobnosti resp. že se osoba dožije věku a neprodělá, resp. prodělá, chorobu, jsou řešením soustavy rovnic Některé klasické úlohy (32) s počátečními podmínkami Některé klasické úlohy (31) a jsou dány výrazy Některé klasické úlohy (34), resp. Některé klasické úlohy (35), kde funkce a jsou dány výrazy Některé klasické úlohy (33).

Pravděpodobnost, že se osoba dožije věku za předpokladu, že choroba se v kohortě neobjevuje (tj. a v důsledku toho také ), je rovna přímo funkci s tj.

Pravděpodobnost, že se osoba dožije věku pokud se choroba vyskytuje, je rovna

Pravděpodobnost dožití věku je tedy součinem pravděpodobnosti dožití věku při přirozené úmrtnosti a faktoru, který závisí pouze na incidenci a letalitě choroby.

Označme dále

Veličina resp. vyjadřuje podmíněnou pravděpodobnost, že osoba věku neprodělala, resp. prodělala, chorobu za podmínky, že se věku dožila.

Poněvadž

(36)

platí rovnost a dále

Relativní zastoupení osob věku které v uvažované kohortě neprodělaly chorobu, je tedy veličina daná formulí Některé klasické úlohy (36), která je současně řešením počáteční úlohy pro Bernoulliovu rovnici

(37)

Vývoj zastoupení osob, které neprodělaly chorobu, tedy nezávisí na přirozené úmrtnosti Úlohu Některé klasické úlohy (37) můžeme vyřešit metodami popsanými v ref{BernoulliRov} a přesvědčit se, že řešení je stejné jako Některé klasické úlohy (36), nebo podrobněji

Zejména pro incidenci choroby a letalitu choroby nezávislé na věku dostaneme

Poznamenejme ještě, že v teorii přežití se funkce nazývají funkce přežití, riziková funkce a kumulativní riziková funkce (v uvedeném pořadí). Pokud

pak pro funkci přežití platí

kde je distribuční funkce náhodné veličiny „věk dožití jedince z kohorty“.

Uvedený model šíření epidemie neštovic publikoval Daniel Bernoulli (1700-1782) v článku

Bernoulli, D. Essai d'une nouvelle analyse de la mortalité causée par la petite vérole et des avantages de l'inoculation pour la prévenir. Hist. Acad R. Sci. Paris. 1760/1766, p.1-45.

v němž hledal odpověď na otázku, zda zavádět očkování proti neštovicím, přestože tato operace někdy končí smrtí.

Na základě tabulek úmrtí, které publikoval královský astronom Edmond Haley (1656-1742)

Halley E. An estimate of the degrees of the mortality of mankind, drawn from curious tables of the births and funerals at the city of Breslaw; with an attempt to ascertain the price of annuities upon lives. Phil. Trans. Roy. Soc. London. 1693, vol. 17, p. 596-610.

odhadl D. Bernoulli hodnoty incidence a letality neštovic nezávislé na věku jako skutečnost, že mu koeficienty vyšly stejné, je náhoda.

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity