Picardova metoda postupných aproximací

Nechť je množina (vektorových) funkcí diferencovatelných na uzavřeném intervalu takových, že Na této množině zavedeme metriku

(metrika stejnoměrné konvergence). Prostor je úplný (sr. Z. Došlá, O. Došlý: Metrické prostory. MU, Brno 1996, I.1.1.2.iv a III.1.3.6.i). Dále definujme zobrazení předpisem:

(2)

Řešení úlohy Obyčejné diferenciální rovnice (4), Obyčejné diferenciální rovnice (5), tedy funkce, která splňuje Obecné vlastnosti obyčejných diferenciálních rovnic (1), je zřejmě pevným bodem zobrazení

Podaří-li se tedy ukázat, že je kontrakce úplného metrického prostoru  z Banachovy věty vyplyne, že existuje jediný  pevný bod tohoto zobrazení, tedy že existuje jediné diferencovatelné řešení úlohy Obyčejné diferenciální rovnice (4), Obyčejné diferenciální rovnice (5) (sr. Z. Došlá, O. Došlý: Metrické prostory. MU, Brno 1996, IV.2. a V.1.).

Picardova - Lindelὃfova věta

Věta 2.1. (Picard [1856-1941] - Lindelὃf [1870-1946]). Buďte Označme

Nechť funkce je spojitá a vzhledem k Lipschitzovská (tj. existuje tak, že platí pro všechna ). Pak existuje právě jedno řešení počátečního problému Obyčejné diferenciální rovnice (4), Obyčejné diferenciální rovnice (5) definované na intervalu

Toto řešení je (stejnoměrnou) limitou posloupnosti funkcí ; tato posloupnost je definována rekurentně vztahem

Důkaz. Je-li funkce diferencovatelná, pak je spojitá (sr. V.Novák: Diferenciální počet v R. MU, Brno 1997, kap. V, věta 1.2). Proto je funkce   diferencovatelná a pro její derivaci platí (sr. V. Novák: Integrální počet v . MU, Brno 2001, 2.4, věta 4.2). To znamená, že zobrazení definované vztahem Obecné vlastnosti obyčejných diferenciálních rovnic (2) zobrazuje množinu do sebe. Buď Na  zavedeme metriku vztahem

Tato metrika je na  ekvivalentní s metrikou stejnoměrné konvergence neboť

Prostor je tedy úplný.

Položme Poněvadž je uzavřená podmnožina množiny  je prostor úplný (sr. Z. Došlá, O. Došlý: Metrické prostory. MU, Brno 1996, III.1.3.3). Zobrazení zobrazuje množinu  do sebe, neboť pro každou funkci platí

Ukážeme, že je kontrakcí prostoru : Pro každé platí

Poněvadž je což znamená, že je kontrakce. Podle Banachovy věty má tedy v jediný pevný bod a tedy existuje jediné diferencovatelné řešení úlohy Obyčejné diferenciální rovnice (4), Obyčejné diferenciální rovnice (5), které je navíc stejnoměrnou limitou posloupnosti funkcí .

Poznámky

Poznámka 2.2. Posloupnost funkcí zavedená ve věte Obecné vlastnosti obyčejných diferenciálních rovnic 2.1 se nazývá Picardova posloupnost postupných aproximací.

Poznámka 2.3. Analogické tvrzení platí, nahradíme-li ve věte Obecné vlastnosti obyčejných diferenciálních rovnic 2.1 interval intervalem nebo intervalem

Poznámka 2.4. Má-li funkce

ohraničené parciální derivace všech složek podle každé z proměnných na množině (zavedené v Obecné vlastnosti obyčejných diferenciálních rovnic 2.1), pak jsou předpoklady Picardovy-Lindelὃfovy věty splněny.

Důkaz. Množina  jakožto uzavřená a ohraničená podmnožina prostoru je kompaktní (sr. Z. Došlá, O. Došlý: Metrické prostory. MU, Brno 1996, III.3.3.16). Z ohraničenosti parciálních derivací funkce plyne existence čísla

Podle věty o střední hodnotě pro funkce více proměnných (sr. Z. Došlá, O. Došlý: Diferenciální počet funkcí více proměnných. MU, Brno 1999, 3.4) pro všechna a    existují čísla ležící mezi a , taková, že

takže funkce  je vzhledem k Lipschitzovská s konstantou

Důsledky

Důsledek 2.5. Má-li (vektorová) funkce

ohraničené parciální derivace všech složek podle každé z proměnných v jistém okolí bodu pak počáteční problém Obyčejné diferenciální rovnice (4), Obyčejné diferenciální rovnice (5) má v okolí jediné řešení.

Důsledek 2.6. Má-li (skalární) funkce v jistém okolí bodu ohraničené parciální derivace podle každé z proměnných  pak počáteční problém Obyčejné diferenciální rovnice (4), Obyčejné diferenciální rovnice (5) má v okolí jediné řešení.

Peanova věta

Věta 2.7. (Peano [1890]). Buďte Označme 

Nechť funkce je spojitá. Pak existuje alespoň jedno řešení počátečního problému Obyčejné diferenciální rovnice (4), Obyčejné diferenciální rovnice (5) definované na intervalu

Důkaz. Viz J. Kalas, M. Ráb: Obyčejné diferenciální rovnice. MU, Brno 2001, str. 67-70.

Užití v numerických metodách

Picardovou metodou postupných aproximací lze odhadnout numerické řešení počáteční úlohy Obyčejné diferenciální rovnice (4), Obyčejné diferenciální rovnice (5). Navíc lze  ukázat, že platí odhad

pro  a Lipschitzovu konstantu splňující z věty Obecné vlastnosti obyčejných diferenciálních rovnic 2.1.

Příklad. Metodou postupných aproximací najdeme řešení diferenciální rovnice

s počáteční podmínkou v 

Řešení. Začneme s funkcí První aproximace splňuje

Všimněte si, že oproti nulté konstantní aproximaci, která splňovala počáteční podmínku v první aproximace splňuje také nutnou podmínku kterou musí splňovat řešení úlohy. Druhá aproximace je

Třetí aproximaci dostaneme jako

Vidíme, že postupné aproximace se stávájí výpočetně složité, vystačíme si proto s třetí aproximací a odhadneme řešení pomocí třetí aproximace jako Protože pro  a je a na množině je a   Lipschitzova konstanta jistě splňuje

protože pro nějaké platí

Odtud a chyba našeho odhadu není větší než

Na obrázku 2.1 jsou zobrazeny postupně aproximace a řešení rovnice s počáteční podmínkou spolu s řešením.

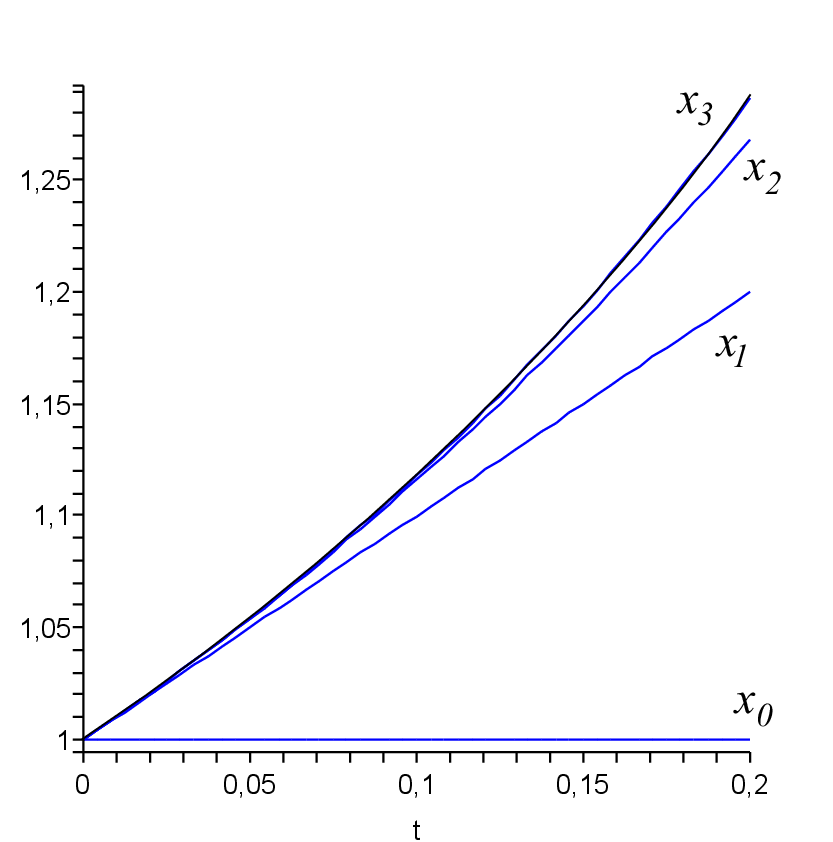Obr. 2.1. Grafy postupných aproximací řešení rovnice s počáteční podmínkou Graf řešení (černě) splývá s grafem

Úlohy k procvičení