Uvažujme reakci nějakého substrátu a enzymu které spolu vytvoří nestabilní komplex z kterého dále vznikne nějaký produkt a volný enzym. Enzymy jsou katalyzátory chemických reakcí, při kterých pomáhají ze substrátu vytvořit produkt přičemž z reakce vycházejí samy v nezměněné formě.

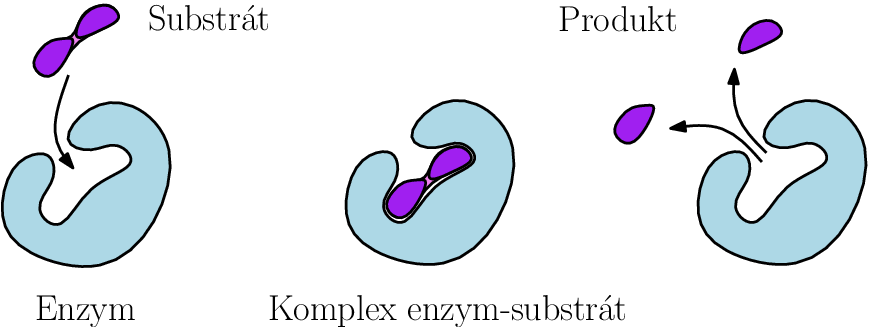
Schematicky tuto reakci můžeme zapsat takto

nebo stručně

přičemž kladné parametry označují reakční rychlosti. První část reakce (vratná reakce tvorby komplexu) byla studována v předchozí kapitole.

Označme

Michaelis a Menten¹ navrhli jako model vývoje koncentrací v čase následující systém čtyř obyčejných nelineárních diferenciálních rovnic

		(2)

Tento model vyjadřuje, že změny koncentrací považujeme za přímo úměrné koncentracím, reakční rychlosti jsou příslušné koeficienty úměrnosti. Budeme předpokládat, že na počátku je koncentrace substrátu rovna a koncentrace enzymu je rovna komplex ani produkt nejsou na počátku přítomny. Spolu se systémem Biochemické modely (2) tedy uvažujeme počáteční podmínky

(3)

Nejprve si všimněme, že veličina se nevyskytuje v prvních třech rovnicích systému Biochemické modely (2). Koncentrace a jsou tedy řešením prvních tří rovnic z Biochemické modely (2), koncentraci produktu můžeme vyjádřit ze čtvrté rovnice integrací

(4)

Množství enzymu se v průběhu reakce nemění a enzym se vyskytuje jednak jako volný a jednak jako vázaný v komplexu To vzhledem k počáteční podmínce Biochemické modely (3) znamená, že by mělo platit pro všechna Model Biochemické modely (2) je skutečně v tomto smyslu adekvátní, neboť

Veličina je prvním integrálem systému Biochemické modely (2) a proto koncentraci enzymu můžeme vyjádřit jako

(5)

a dosadit do první a třetí rovnice systému Biochemické modely (2). Dostaneme

(6)

Časový průběh koncentrací substrátu a komplexu je tedy řešením systému dvou obyčejných autonomních nelineárních diferenciálních rovnic Biochemické modely (6) s počáteční podmínkou

(7)

průběh koncentrací volného enzymu a produktu je dána výrazy Biochemické modely (5) a Biochemické modely (4).

Změníme měřítko tak, aby všechny veličiny byly bezrozměrné, tj. zavedeme substituci

(8)

veličina vyjadřuje koncentraci substrátu a veličina koncentraci komplexu v jednotkách počáteční koncentrace substrátu a enzymu. Časová jednotka je určena rychlostí reakce substrátu a enzymu. Platí

Při označení

(9)

se systém Biochemické modely (6) substitucí Biochemické modely (8) transformuje na systém

(10)

s počátečními podmínkami

(11)

Poznamenejme, že parametry a jsou kladné a

Úlohu Biochemické modely (10), Biochemické modely (11) nelze řešit explicitně. Proto ji budeme analyzovat ve fázovém prostoru. Nulklinu proměnné můžeme vyjádřit jako graf funkce

Derivace

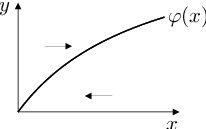je pro kladná, pro záporná. Situace je znázorněna na obrázku:

Podobně vyjádříme -nulklinu jako graf funkce

a vyšetříme znaménka derivací:

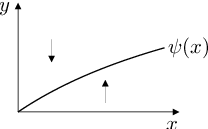Poněvadž a pro všechna vypadá fázový portrét systému Biochemické modely (10) tak, jak je znázorněno na obr. Biochemické modely 3 Vidíme, že systém Biochemické modely (10) má jediný stacionární bod a že množina je jeho pozitivně invariantní množinou (na úsečce směřují trajektorie nahoru, na úsečce dolů, na úsečce směřují trajektorie doprava a na úsečce doleva). Variační matice systému Biochemické modely (10) v obecném bodě je

takže ve stacionárním bodě platí

neboť Stacionární bod je podle Kvalitativní vlastnosti řešení dvourozměrného autonomního systému Autonomní systémy a kvalitativní teorie (5) stabilní uzel (což bylo vidět z fázového portrétu i bez výpočtů). Pro řešení úlohy Biochemické modely (10), Biochemické modely (11) tedy platí

Výsledkem reakce je vyčerpání veškerého substrátu nebude volný ani vázaný s enzymem v komplexu Z trajektorie řešení úlohy Biochemické modely (10), Biochemické modely (11), která je rovněž zobrazena na následujícím obrázku, je také vidět, že složka řešení této úlohy k nule monotonně klesá. Složka nejdříve roste, v jistém čase dosáhne svého maxima

a pak monotonně klesá k nule.

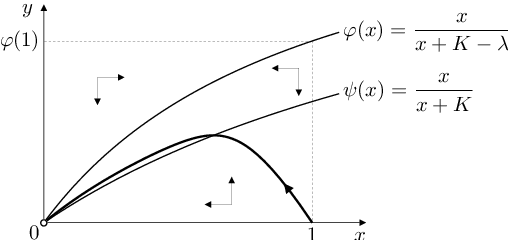Obr. 3. Fázový portrét systému Biochemické modely (10) a jeho trajektorie s počátečním bodem Biochemické modely (10) a hodnotou parametru

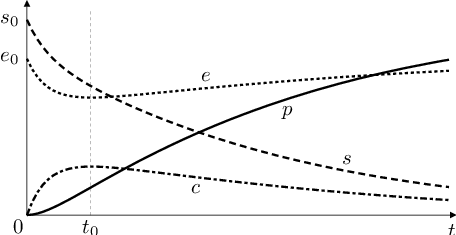
Nyní můžeme kvalitativně popsat řešení původní úlohy Biochemické modely (2), Biochemické modely (3), viz obr. následující obrázek. Koncentrace substrátu monotonně klesá k nule. Koncentrace komplexu roste ke své maximální hodnotě, která je menší než byla počáteční koncentrace enzymu a pak monotonně klesá k nule. Koncentrace volného enzymu nejprve klesá, v okamžiku kdy je koncentrace komplexu maximální, dosáhne svého minima a pak monotonně roste k počáteční hodnotě Koncentrace produktu roste z nulové hodnoty, růst se nejprve zrychluje (funkce je konvexní), od okamžiku se začne zpomalovat (funkce je konkávní).

Obr. 4. Průběh řešení úlohy Biochemické modely (2),Biochemické modely (3).

¹ L.Michaelis, M. I. Menten. Die Kinetik der Invertinwirkung. Biochem. Z. 49, 333-369, 1913

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity