Odhady řešení

Definice 4.1. Řešení úlohy Obyčejné diferenciální rovnice (1), Obyčejné diferenciální rovnice (2) se nazývá maximální řešení, jestliže pro každé řešení této úlohy platí pro všechna v nichž jsou obě řešení definována. 
Řešení úlohy Obyčejné diferenciální rovnice (1), Obyčejné diferenciální rovnice (2) se nazývá minimální řešení, jestliže pro každé řešení  této úlohy platí pro všechna v nichž jsou obě řešení definována.

Příklad. Uvažujme počáteční úlohu

(8)

Přímým výpočtem ověříme, že kterákoliv z funkcí

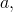
kde jsou nezáporné konstanty, je jejím úplným řešením. Minimální a maximální řešení úlohy Obecné vlastnosti obyčejných diferenciálních rovnic (8) tedy jsou funkce

řešení je znázorněno na obrázku 3.3 a).

Věta 4.2. (srovnávací). Nechť      Nechť dále   je spojitá funkce a je spojitá funkce taková, že pro Buď a maximální řešení úlohy

na intervalu

Pak každé úplné řešení úlohy Obyčejné diferenciální rovnice (4), Obyčejné diferenciální rovnice (5) je definováno pro všechna a platí

Důkaz. Viz J. Kalas, M. Ráb: Obyčejné diferenciální rovnice. MU, Brno 2001, str. 91.

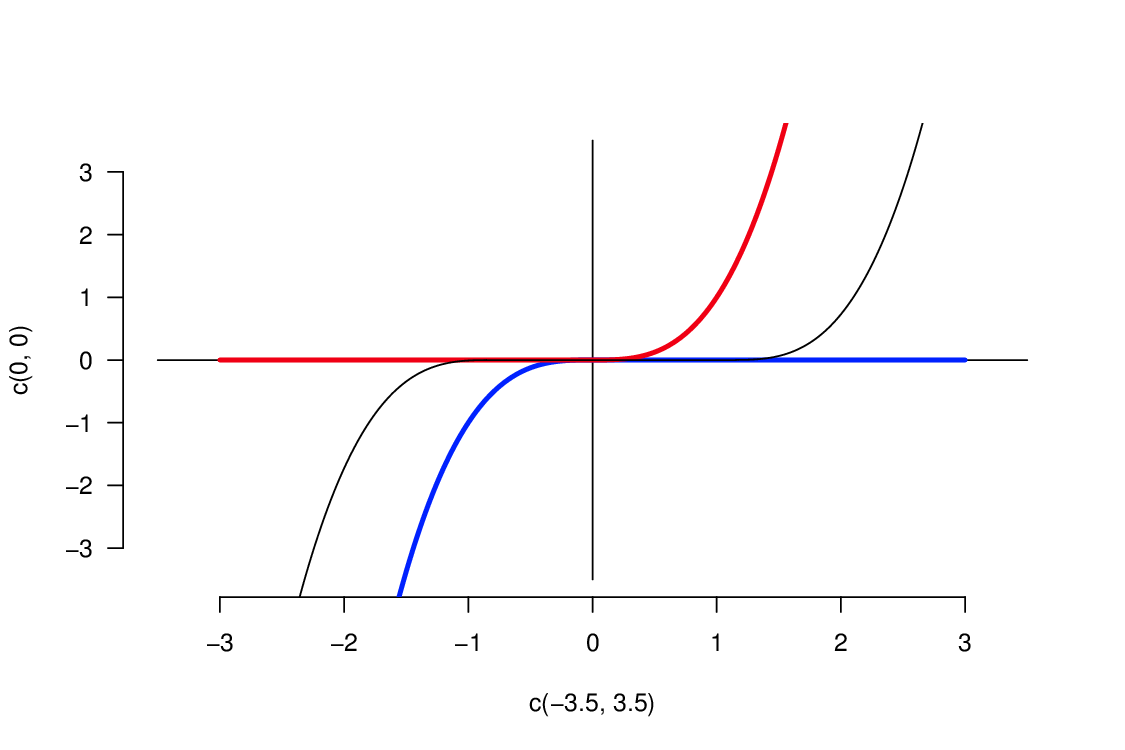a)	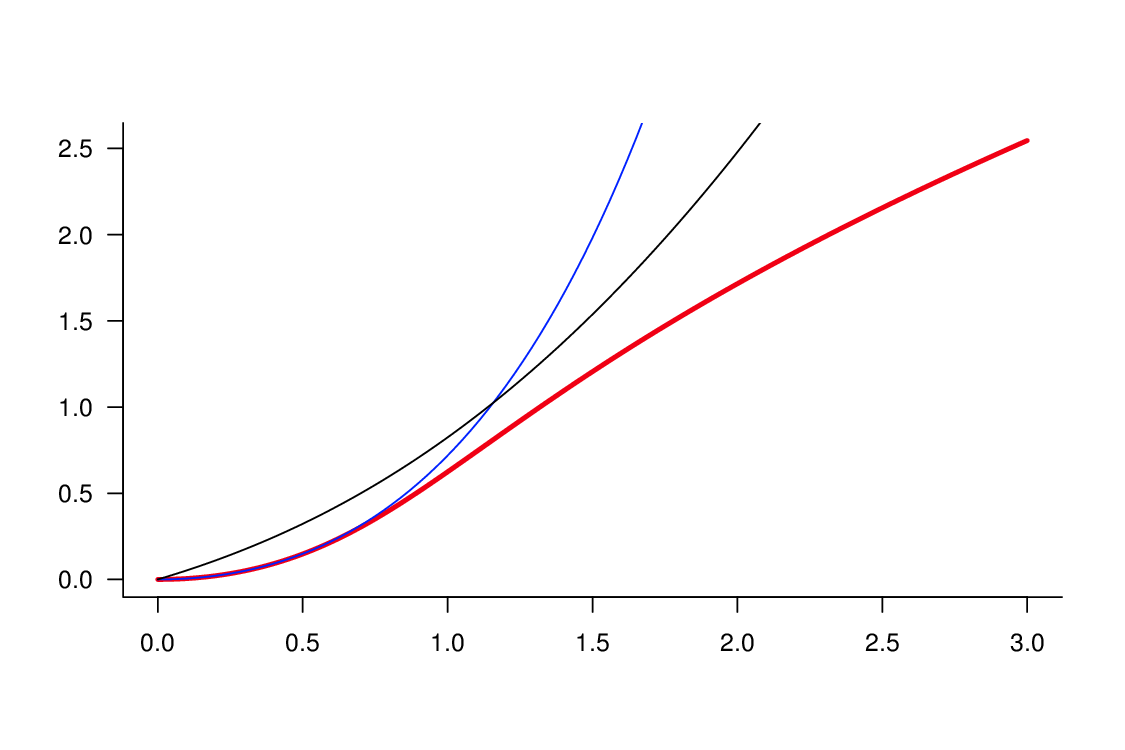b)
Obr. 3.3. a) Maximální a minimální řešení počáteční úlohy Obecné vlastnosti obyčejných diferenciálních rovnic (8). b) Odhady řešení úlohy  Obecné vlastnosti obyčejných diferenciálních rovnic (9) s hodnotami

Příklad. Najdeme odhad řešení počátečního problému

(9)

na intervalu

Pravou stranu rovnice můžeme chápat jako funkci jedné proměnné s jedním parametrem Standardními metodami diferenciálního počtu najdeme globální maximum a minimum této funkce; konkrétně, pro každé  platí

Odtud plyne že

Počáteční úloha

má podle ref{rovprimfce} jediné řešení

a podle srovnávací věty Obecné vlastnosti obyčejných diferenciálních rovnic 4.2 platí pro všechna

Řešení úlohy Obecné vlastnosti obyčejných diferenciálních rovnic (9) pro lze odhadnout i jiným způsobem. V takovém případě totiž platí

Jediné řešení počáteční úlohy

pro nehomogenní lineární rovnici je podle ref{elreslinrov} rovno

a podle srovnávací věty Obecné vlastnosti obyčejných diferenciálních rovnic 4.2 platí pro všechna

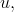
Poznamenejme ještě, že nelze říci, že by některý z uvedených odhadů řešení úlohy Obecné vlastnosti obyčejných diferenciálních rovnic (9) byl lepší než druhý. Situace je znázorněna na obrázku 3.3 b).

Důsledek 4.3. Nechť symboly mají stejný význam jako v Obecné vlastnosti obyčejných diferenciálních rovnic 4.2. Nechť funkce je spojitá a nechť existuje spojitá funkce taková, že

Pak pro každé takové, že 

jsou úplná řešení úlohy Obyčejné diferenciální rovnice (4), Obyčejné diferenciální rovnice (5) definována na celém intervalu a platí

Důkaz. Plyne z Obecné vlastnosti obyčejných diferenciálních rovnic 4.2 volbou

Jediné úplné (tedy maximální) řešení úlohy  je podle části Lineární rovnice

Úlohy k procvičení