Rybolov s konstantním úlovkem za jednotku času

Ryby však nejsou ponechány svému vývoji, jejich populace je využívána. Rybolov můžeme popsat tak, že z populace ryb je pravidelně odstraňován jistý počet jedinců, za jednotku času je vyloveno určité množství ryb. (To si lze například představit tak, že u jezera žijí rybáři, kteří mají pevně daný počet loděk, každý den vyrazí na lov a loví tak dlouho, až své čluny naplní.) Označme množstv

Ryby však nejsou ponechány svému vývoji, jejich populace je využívána. Rybolov můžeme popsat tak, že z populace ryb je pravidelně odstraňován jistý počet jedinců, za jednotku času je vyloveno určité množství ryb. (To si lze například představit tak, že u jezera žijí rybáři, kteří mají pevně daný počet loděk, každý den vyrazí na lov a loví tak dlouho, až své čluny naplní.) Označme množství ryb ulovených za jednotku času; parametr je kladný. Pak vývoj populace ryb, jejíž velikost byla na začátku rovna hodnotě je popsán počáteční úlohou pro diferenciální rovnici

(12)

Základní otázkou je, zda rybolov je udržitelný, tj. zda v dostatečně dlouhém časovém horizontu bude populace ryb přežívat nebo ji lov vyhubí.

Rovnice v úloze Základní modely populační dynamiky (12) je Riccatiho a řešíme ji tedy substitucí

(13)

Dosazení do rovnice Základní modely populační dynamiky (12) dává

tj.

Odtud snadnou úpravou dostaneme lineární homogenní rovnici druhého řádu s konstantními koeficienty

(14)

Její charakteristická rovnice je

(15)

Označme Pak neboť parametry jsou kladné. Při řešení úlohy Základní modely populační dynamiky (12) rozlišíme tři případy podle znaménka veličiny

(i) 

V tomto případě má charakteristická rovnice Základní modely populační dynamiky (15) dva reálné různé kořeny

a protože  jsou oba kořeny kladné. Obecné řešení lineární rovnice Základní modely populační dynamiky (14) je

kde jsou nějaké konstanty. Platí tedy

Odtud a z transformačního vztahu Základní modely populační dynamiky (13) dostaneme obecné řešení rovnice z úlohy Základní modely populační dynamiky (12) ve tvaru

Konstanty získáme z počáteční podmínky v úloze Základní modely populační dynamiky (12):

To je jedna rovnice pro dvě neznámé a hodnoty z ní nelze vypočítat. Lze však určit jejich poměr

Řešení úlohy Základní modely populační dynamiky (12) je tedy dáno formulí

neboť

Nyní můžeme vyšetřovat průběh funkce v závislosti na počáteční hodnotě (parametru) Pokud je pak je funkce kladná pro jakoukoliv hodnotu nezávisle proměnné a platí

zejména pro je funkce konstantní, Rybolov zredukuje velikost populace ryb na hodnotu

Pokud je pak je funkce konstantní,

Ovšem, pokud je pak pro

je To znamená, že lov ryby vyhubí.

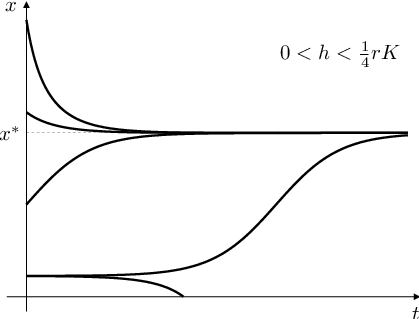
Řešení počáteční úlohy Základní modely populační dynamiky (12) s hodnotou a s různými počátečními hodnotami je zobrazeno na obrázku vlevo nahoře.

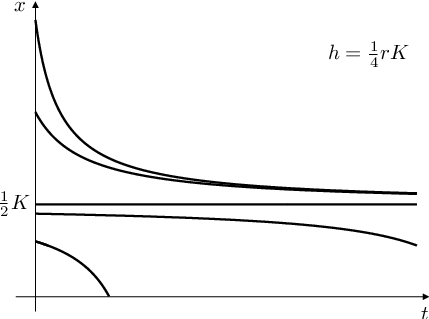
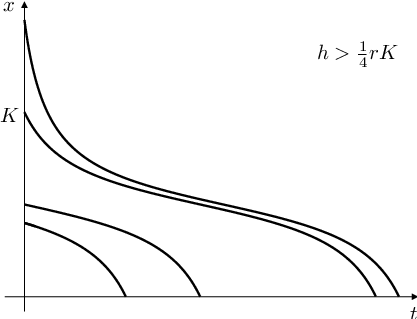
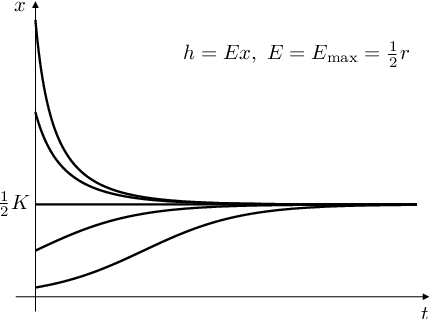
Obr. 1. Modely rybolovu. Rybolov s konstantním úlovkem za časovou jednotku, tj. řešení úlohy Základní modely populační dynamiky (12) pro různé hodnoty intenzity lovu h a pro různé počáteční hodnoty (nahoře a vlevo dole). Rybolov s konstantním loveckým úsilím, tj. řešení úlohy Základní modely populační dynamiky (17) s úsilím E přinášejícím maximální udržitelný úlovek pro různé počáteční hodnoty  (vpravo dole).

(ii) 

V tomto případě má charakteristická rovnice Základní modely populační dynamiky (15) dvojnásobný reálný kladný kořen Obecné řešení lineární rovnice Základní modely populační dynamiky (14) v tomto případě je rovno

Pro toto řešení musí platit jinak by transformace Základní modely populační dynamiky (13) nebyla definována v pravém okolí počáteční hodnoty. Odtud plyne, že a řešení můžeme upravit na tvar

kde Derivace řešení je rovna

a obecné řešení rovnice z úlohy Základní modely populační dynamiky (12) je

Toto řešení má splňovat počáteční podmínku v úloze Základní modely populační dynamiky (12), takže

Řešení úlohy Základní modely populační dynamiky (12) je tedy v případě dáno formulí

Pokud je toto řešení kladné pro každé Zejména pro je řešení konstantní, Pokud naopak je řešení kladné pouze pro kde

a Řešení úlohy Základní modely populační dynamiky (12) v případě pro různé počáteční hodnoty je znázorněno na obr. Základní modely populační dynamiky 1 vpravo nahoře.

V případě je tedy rybolov udržitelný pouze pokud byla počáteční velikost populace ryb alespoň na polovině úživnosti prostředí. V takovém případě rybolov dlouhodobě udržuje velikost populace na hodnotě neboť

Pokud je počáteční velikost populace ryb menší, lov ryby vyhubí v čase

(iii) 

V tomto případě má charakteristická rovnice Základní modely populační dynamiky (15) komplexně sdružené kořeny

a obecné řešení lineární rovnice Základní modely populační dynamiky (14) je tvaru

kde jsou konstanty. Jeho derivace je rovna

a řešení rovnice z úlohy Základní modely populační dynamiky (12) podle transformačního vztahu Základní modely populační dynamiky (13) je dáno formulí

Aby toto řešení splnilo počáteční podmínku v úloze Základní modely populační dynamiky (12), musí platit

tedy

Řešení úlohy Základní modely populační dynamiky (12) je nyní kladné pouze na intervalu kde je nejmenší kladné řešení rovnice

tedy

Pro tedy rybolov nemůže být udržitelný. Řešení úlohy Základní modely populační dynamiky (12) v případě pro různé počáteční hodnoty je znázorněno na obr. Základní modely populační dynamiky 1 vlevo dole.

Z rozboru řešení modelu Základní modely populační dynamiky (12) plyne, že rybolov může být udržitelný pouze v případě, že není příliš intenzivní a počáteční populace ryb je dostatečně velká, konkrétně když

Maximální udržitelný úlovek je tedy

(16)