Užití Laplaceovy transformace na řešení diferenciálních rovnic

Věta o obrazu derivace ukazuje výhody Laplaceovy transformace. Jestliže se předmět zderivuje, jeho Laplaceův obraz se vynásobí veličinou Operace derivování podle v prostoru předmětu se převádí na algebraickou operaci násobení v prostoru obrazu. Diferenciální rovnice představuje vztah mezi předmětem a jeho derivacemi, přitom obraz předmětu pak musí splňovat jednodušší algebraickou rovnici, jejíž řešení je možné získat běžnými algebraickými úpravami. Laplaceova transformace tak převádí diferenciální rovnice nebo systémy na rovnice algebraické. Problémem však je získat k danému obrazu původní předmět. K tomu je třeba najít zpětnou Laplaceovu transformaci (inverzní trasformaci k Laplaceově). Jak bude vidět v následujícím textu, u lineárních diferenciálních rovnic vede řešení algebraické rovnice na obraz ve tvaru racionální lomené funkce, což dává tušit, že použijeme metodu rozkladu racionální lomené funkce na parciální zlomky, jejichž předměty jsou ve „slovníku“.

Nechť je dána lineární diferenciální rovnice -tého řádu s konstantními koeficienty

kde je hledaná funkce, jsou konstanty a je funkce, která je předmětem standardního typu. (V předchozí výukové jednotce týkající se lineárních diferenciálních rovnic jde o rovnici Lineární rovnice (25).)

Nechť navíc jsou daná reálná čísla. Hledejme funkci která by diferenciální rovnici vyhovovala pro všechna   pro něž je  spojitá, a která by i se svými derivacemi až do řádu včetně byla spojitá v otevřeném intervalu a která by pro vyhovovala počátečním podmínkám Je-li funkce  i se svými derivacemi spojitá v polouzavřeném intervalu píšeme obvykle počáteční podmínky ve tvaru Předpokládejme, že takové řešení existuje právě jedno. Označme Laplaceův obraz hledaného řešení  Podle věty o obrazu derivace:

Protože Laplaceova transformace je lineární operátor, platí pro obraz levé strany rovnice

Rovnají-li se dvě funkce, musí se rovnat i jejich Laplaceovy obrazy. Označíme-li tedy můžeme napsat

Tuto rovnici nazýváme obrazem diferenciální rovnice. Můžeme ji ještě přepsat ve tvaru

Z této algebraické rovnice můžeme vypočítat 

Použijeme-li ještě stručnějšího označení ( je tedy mnohočlen právě -tého stupně) a 

( je tedy mnohočlen stupně nejvýše ), můžeme napsat

Tím jsme získali obraz řešení rovnice. Řešení  původní rovnice tedy splňuje Úlohu najít k dané funkci  obecně komplexní proměnné předmět  tak, aby  nazýváme zpětnou Laplaceovou transformací a píšeme

Při hledání předmětu k danému obrazu používáme pravidel transformace uvedených v části Základní vlastnosti Laplaceovy transformace. Je zřejmé, že zpětná Laplaceova transformace je také lineární operátor, platí tedy např.  jestliže existují 

potom

kde Tento vzorec lze rozšířit na libovolný konečný počet členů.

Podobně jestliže

potom

Obdobně lze při zpětné transformaci užít i ostatních dříve uvedených vět.

Příklad 3.1. Užití Laplaceovy transformace si ukážeme na příkladu oscilátoru, tentokrát buzeného vnější silou. Poprvé jsme se s harmonickým oscilátorem setkali v posledním příkladu první výukové jednotky. Nyní máme těleso o hmotnosti 1 kg je zavěšené na pružině, jejíž tuhost je 100 Nm Těleso začne po vychýlení z rovnovážné polohy kmitat. Po celou dobu kmitání působí na oscilátor vnější síla Sestavíme příslušnou diferenciální rovnici a nalezneme řešení  za počátečních podmínek a Odpor prostředí a případné tření zanedbáváme. Oscilátory si můžeme přestavovat takto fyzikálně, je třeba si však uvědomit, že na obdobnou diferenciální rovnici vedou modely elektrických obvodů, s oscilátory se setkáváme např. při přenosu signálu se zpětnou vazbou, např. neuronem, v biochemických procesech v buňce a podobně. Tyto modely budou jistě složitější, některé si představíme v dalších výukových jednotkách, ale k jejich pochopení je důležité rozumět základním modelům oscilátoru.

Řešení. Neuvažujeme-li odpor prostředí a tření, je kmitání popsáno rovnicí 

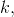
Dosazením za   a  ze zadání dostáváme příslušnou diferenciální rovnici

Laplaceovou transformací levé i pravé strany rovnice dostáváme

takže

A zpětnou transformací nakonec dostaneme řešení úlohy ve tvaru

Z tvaru funkce   jež je řešením úlohy, vidíme, že těleso zavěšené na pružině bude pokračovat v kmitavém pohybu a amplituda výchylky jeho pohybu s rostoucím časem poroste, což je dáno buzením vnější silou.

Příklad 3.2. Vyřešíme předchozí příklad za předpokladu, že pohyb je brzděn odporem prostředí a třením. Předpokládáme, že souhrnná hodnota součinitele odporu těchto jevů byla experimentálně stanovena na 25.

Řešení. V případě, kdy uvažujeme vliv odporových sil, je kmitavý pohyb popsán rovnicí

Dosazením za a  dostáváme

Laplaceovou transformací tedy dostáváme

takže

Každý ze sčítanců nyní rozložíme na parciální zlomky. Rozkladem prvního členu dostaneme

Dosazením dostáváme

a dosazením dostaneme

Nakonec porovnáme koeficienty u

a porovnáním koeficientů u 

Rozkladem druhého členu dostáváme

Dosazením  dostaneme

a porovnáním koeficientů u 

Rozkladem na parciální zlomky jsme nakonec dostali 

Odtud zpětnou Laplaceovou transformací dostáváme řešení úlohy ve tvaru

Funkce se limitně blíží nule pro Z tvaru funkce  popisující kmitání tělesa lze tedy usoudit, že oproti předchozímu příkladu je pohyb vybuzený vnější silou brzděn odporem prostředí a třením. Vzhledem k členu jenž je součástí řešení, bude pohyb tělesa směřovat ke kmitání s velmi nízkou amplitudou výchylky.

Příklad 3.3. Nyní si ukážeme, že také elektrický obvod může být popsán podobnou rovnicí. Uvažujme  elektrický obvod, který je tvořen sériovým zapojením cívky o indukčnosti   a kondenzátoru o kapacitě V takovém obvodě se náboj, proud a napětí mění harmonicky a říkáme, že obvod kmitá. Obvod je navíc podroben za pomoci vnějšího zdroje napětí vynuceným kmitům

které působí jen na počátku a pak ustanou. Toto ukážeme nalezením řešení příslušné diferenciální rovnice, tj. nalezneme řešení za počátečních podmínek a Odpor drátů a součástek zapojených v obvodu zanedbáváme.

Řešení. Průchodem proudu a vzniká elektromagnetické pole, které na cívce indukuje napětí pro které je tím větší, čím větší je změna proudu, přesněji

přičemž velikost proudu je dána změnou náboje Na kondenzátoru zase musí platit lineární vztah mezi napětím a nábojem Je zřejmé, že v sériovém obvodu bude pro napětí platit

dosazením tedy dostáváme

Kmity obvodu s nulovým odporem tedy popisuje rovnice

Dosazením za a ze zadání dostáváme příslušnou diferenciální rovnici

Funkci  lze zapsat pomocí Heavisideovy funkce  a posunuté Heavisideovy funkce ve tvaru

Je-li totiž  funkce, která je nulová pro a rovna jedné pro pak funkce  je rovna nule pro a rovna jedné pro
Z obrazu Heavisideovy funkce a věty Laplaceova transformace 2.10 pak plyne

Nyní použijeme Laplaceovu transformaci na diferenciální rovnici

tedy

První a třetí člen rozložíme na parciální zlomky. Rozkladem prvního členu dostáváme

Dosazením dostaneme Porovnáme koeficienty u

Porovnáním koeficientů u  je a nakonec porovnáním u  dostáváme

Rozkladem třetího členu dostaneme

Dosazením dostáváme Porovnáme koeficienty u 

a nakonec porovnáním u je
Takže rozkladem na parciální zlomky jsme dostali

Inverzní transformací dostáváme řešení úlohy pro  ve tvaru

což můžeme také zapsat ve tvaru

jejíž derivací je proud v obvodu

Úlohy k procvičení