Pes pronásleduje zajíce. Zajíc se pohybuje rovnoměrně přímočaře rychlostí pes běží ve směru k zajíci rovnoměrnou rychlostí Určete tvar dráhy psa a čas za který pes zajíce dohoní.

Zvolíme orthonormální souřadnou soustavu tak, aby se zajíc pohyboval po druhé ose souhlasně s její orientací a na počátku, tj. v čase se zajíc nacházel v bodě a pes v bodě Nechť pro určitost je případ je triviální a v případě bude tvar dráhy zřejmě obrazem tvaru pro v osové symetrii kolem druhé souřadné osy.

(a)

(b)

(c)

(d)

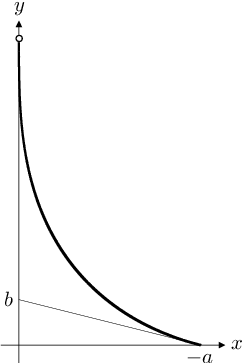
Obr. 5.1. (a) K odvození rovnice „psí křivky“. Vektor rychlosti zajíce má v každém okamžiku souřadnice vektor rychlosti psa má v každém okamžiku velikost a v čase směřuje k zajíci, tj. je rovnoběžný s vektorem o souřadnicích

(b) „Psí křivka“ pro .

(d) „Psí křivka“ pro

Situace je znázorněna na Obr. 5.1 a). Dráhu psa vyjádříme jako funkci V čase je a

tj.

(18)

Pes k zajíci směřuje od začátku, tj.

(19)

V jistém čase se pes nachází v bodě a zajíc v bodě Poněvadž pes stále směřuje k zajíci, platí

neboli

(20)

Za čas urazí pes dráhu délky Této hodnotě tedy musí být rovna délka křivky (grafu funkce) od bodu po bod tedy

Z této rovnosti vyjádříme a dosadíme do Některé klasické úlohy (20),

(21)

Označíme

(22)

Podle předpokladu je Obě strany rovnosti Některé klasické úlohy (21) zderivujeme podle Dostaneme

a po úpravě

(23)

Dráha psa je tedy řešením neautonomní nelineární diferenciální rovnice druhého řádu Některé klasické úlohy (23) s počátečními podmínkami Některé klasické úlohy (18),Některé klasické úlohy (19).

Rovnice Některé klasické úlohy (23) je typu ref{snizradK}. Proto zavedeme novou neznámou funkci Dosadíme ji do rovnice Některé klasické úlohy (23) a počáteční podmínky Některé klasické úlohy (19). Po snadné úpravě dostaneme počáteční úlohu

Jedná se o rovnici se separovanými proměnnými. Řešení úlohy v implicitním tvaru tedy podle ref{rovseppr} je

Integrací dostaneme

a odtud

kde

(24)

Poněvadž a funkce splňuje podmínku Některé klasické úlohy (18), dostaneme řešení úlohy integrací poslední rovnosti, tedy

Za konstanty a dosadíme z rovností Některé klasické úlohy (22) a Některé klasické úlohy (24). Po úpravách dostaneme „psí křivku“ ve tvaru

Nalezená funkce je sudá, vyjadřuje tedy tvar dráhy psa pro i pro v prvním případě bychom za definiční obor považovali interval ve druhém interval

Pes dostihne zajíce v bodě To znamená, že zajíc rychlostí urazí dráhu délky a čas, za který pes zajíce dohoní, je tedy roven

„Psí křivku“ („courbe chien“) jako první studoval v roce 1732 francouzský matematik Pierre Bouger (ten je známější jako účastník expedice do Peru v roce 1735, která změřila délku jednoho stupně zeměpisné délky na rovníku). Křivka je nejjednodušším případem křivek sledování (pursuit curves, pojem poprvé použil George Boole ve svém spisu „Treatise on Differential equations“ v roce 1859), které jsou definovány takto: jestliže body a se pohybují rovnoměrně, bod po dané křivce a směr pohybu bodu stále míří k bodu pak bod opisuje křivku sledování.

Úloha bývá někdy formulována tak, že pes sleduje svého pána, nebo že liška honí králíka.

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity