Autonomní systémy v rovině

V tomto oddílu se budeme zabývat systémem Autonomní systémy a kvalitativní teorie (1) pro tedy systémem

(5)

Definice 2.1. Křivka zadaná implicitně rovnicí (resp. ) se nazývá -nulklina (resp. -nulklina) rovnice Autonomní systémy a kvalitativní teorie (5).

Průsečík nulklin je stacionární bod, tečna k trajektorii v jejím průsečíku s -nulklinou (resp. -nulklinou) je rovnoběžná s osou (resp. ).

Definice 2.2. (typy stacionárních bodů v rovině). Stacionární bod systému Autonomní systémy a kvalitativní teorie (5) se nazývá

	bod rotace, jestliže v jeho libovolném okolí leží cyklus, obsahující  ve svém vnitřku,
	střed, jestliže existuje jeho ryzí okolí takové, že každá trajektorie s je cyklem obsahujícím  ve svém vnitřku (střed je speciálním případem bodu rotace),
	ohnisko, jestliže existuje jeho ryzí okolí takové, že pro každou trajektorii s  platí  a pro orientovaný úhel který svírá vektor s nějakým pevným vektorem platí (trajektorie se přibližuje ke stacionárnímu bodu (nebo se od něho vzdaluje) po spirále),
	uzel, jestliže existuje jeho ryzí okolí takové, že pro každou trajektorii s  platí a pro orientovaný úhel  který svírá vektor  s nějakým pevným vektorem existuje vlastní nebo
	sedlo, jestliže existuje jen konečný počet trajektorií takových, že

Stacionární body lineárního homogenního autonomního systému

Lineární homogenní autonomní systém je lineární homogenní systém s konstantní maticí. Budeme se tedy zabývat dvojrozměrným systémem

(6)

Označme

Pokud má systém Autonomní systémy a kvalitativní teorie (6) jediný stacionární bod Vlastní čísla matice jsou kořeny charakteristické rovnice

(7)

tedy při označení je

(i) 

(i.1) 

V tomto případě je a kořeny charakteristické rovnice Autonomní systémy a kvalitativní teorie (7) jsou ryze imaginární, takže řešení systému Autonomní systémy a kvalitativní teorie (6) s počáteční podmínkou je

pro vhodné konstanty přičemž 

Jedná se o parametrické vyjádření elips se středem každá trajektorie je tedy cyklem se stacionárním bodem ve svém vnitřku. To znamená, že stacionární bod je střed.

(i.2) 

(i.2.a) 

V tomto případě je charakteristická rovnice Autonomní systémy a kvalitativní teorie (7) má dva různé komplexně sdružené kořeny a systém Autonomní systémy a kvalitativní teorie (6) s počáteční podmínkou  má řešení

kde jsou vhodné konstanty, přičemž

Jedná se o parametrické vyjádření spirály, která se „navíjí“ na stacionární bod  nebo se z něho „odvíjí“.

Pokud  pak

pokud  pak

(i.2.b) 

Nechť je řešením systému Autonomní systémy a kvalitativní teorie (6) a označme úhel, který svírá přímka procházející body   s vodorovnou osou. Platí

V tomto případě je a Charakteristická rovnice Autonomní systémy a kvalitativní teorie (6) má dva reálné různé kořeny takové, že oba mají stejné znaménko jako Nechť pro určitost a

je vlastní vektor příslušný k vlastní hodnotě resp. Alespoň jedna ze souřadnic každého z vlastních vektorů je nenulová. Obecné řešení systému Autonomní systémy a kvalitativní teorie (6) s počáteční podmínkou  je

přitom alespoň jedna z konstant je nenulová.

Je-li pak a

je-li pak a

Pokud pak

a pokud  pak

Analogicky, pokud pak

Pokud  pak

Stacionární bod  je v tomto případě uzel. Směrový vektor polotečny k libovolné trajektorii ve stacionárním bodě je vlastním vektorem matice

(i.2.c) 

V tomto případě je neboť charakteristická rovnice Autonomní systémy a kvalitativní teorie (7) má dvojnásobný kořen a systém Autonomní systémy a kvalitativní teorie (6) s počáteční podmínkou  má řešení

kde jsou nějaké konstanty, z nichž aspoň dvě jsou nenulové. Proto platí

Je-li pak

a tedy

Je-li pak analogicky

Stacionární bod  je v tomto případě uzel. Nyní však již obecně neplatí, že směrový vektor polotečny k trajektorii ve stacionárním bodě je vlastním vektorem matice v případě (tj. pokud vlastní hodnotě matice  přísluší dva lineárně nezávislé vlastní vektory) je každá přímka procházející bodem  polotečnou nějaké trajektorie.

Je-li pak z podmínky tj. plyne, že

Vlastní hodnotě přísluší jediný (až na násobek skalárem) vlastní vektor

Je-li pak z podmínky plyne tj.

Matice

má pro  jednoznačně určený vlastní vektor

příslušný k vlastní hodnotě  pro

je každý vektor vlastním vektorem matice

příslušným k vlastní hodnotě

Nyní můžeme předchozí tvrzení upřesnit. Je-li pak směrový vektor polotečny k trajektorii ve stacionárním bodě  je vlastním vektorem matice  příslušným k vlastní hodnotě Je-li  pak každý nenulový vektor  je směrovým vektorem polotečny k nějaké trajektorii ve stacionárním bodě 

(ii)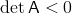 

V tomto případě je což znamená, že rovnice Autonomní systémy a kvalitativní teorie (7) má dva reálné různé kořeny  Poněvadž mají tyto kořeny opačná znaménka. Nechť pro určitost Označme resp. vlastní vektor matice  příslušný k vlastní hodnotě  resp.  Obecné řešení systému Autonomní systémy a kvalitativní teorie (6) je podle ref{rSLRk}

kde jsou nějaké konstanty. Pro je

pro je

a pro je

To znamená, že stacionární bod  je sedlo. Směrový vektor polotečny ke trajektorii, která směřuje ke stacionárnímu, resp. od stacionárního, bodu, je vlastním vektorem matice  příslušným k záporné, resp. kladné, vlastní hodnotě.

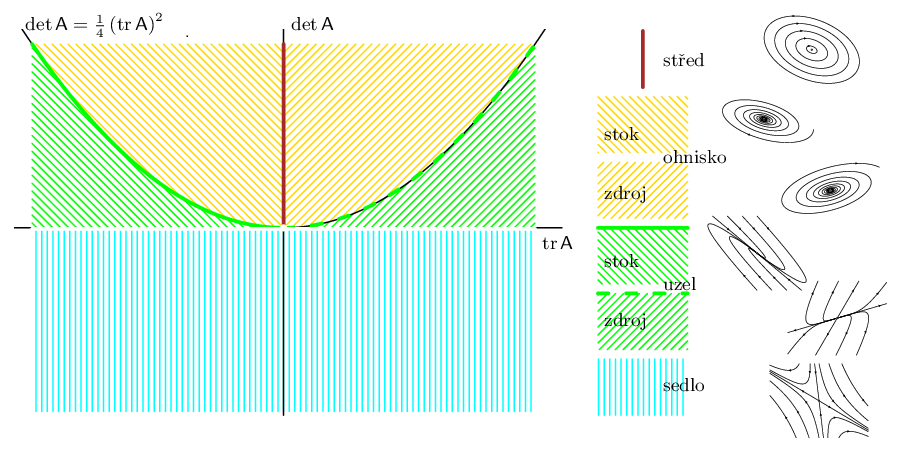
Výsledky provedené analýzy lineárního dvourozměrného systému Autonomní systémy a kvalitativní teorie (6) s konstantní maticí jsou shrnuty graficky na následujícím obrázku.

Obr. 2.1. Typy izolovaných stacionárních bodů dvourozměrného autonomního lineárního homogenního systému Autonomní systémy a kvalitativní teorie (6) v závislosti na hodnotách stopy a determinantu jeho matice.