Definice jednorozměrného GLM

Předchozí pasáž nám poskytla motivaci pro hledání obecnějšího modelu, než je model lineární. Uveďme nyní již samotnou definici zobecněného lineárního modelu a poté několik příkladů pro lepší názornost.

Definice 3.1. (Zobecněný lineární model). Mějme náhodný výběr

a nechť rozdělení závisí na pevných vektorech

prostřednictvím neznámého vektoru parametrů

Matice

má rozměr a hodnost

Říkáme, že  se řídí zobecněným lineárním modelem (Generalized Linear Model), jestliže dále platí:

(1)	rozdělení  je exponenciálního typu s regulární hustotou tvaru (3)
(2)	parametr závisí na a prostřednictvím parametru (4)   který nazveme lineární prediktor.
(3)	Existuje známá ryze monotónní diferencovatelná funkce tzv. linkovací funkce (link function), a platí (5)   Řekneme, že linkovací funkce je kanonická, pokud

Matici nazýváme maticí plánu.

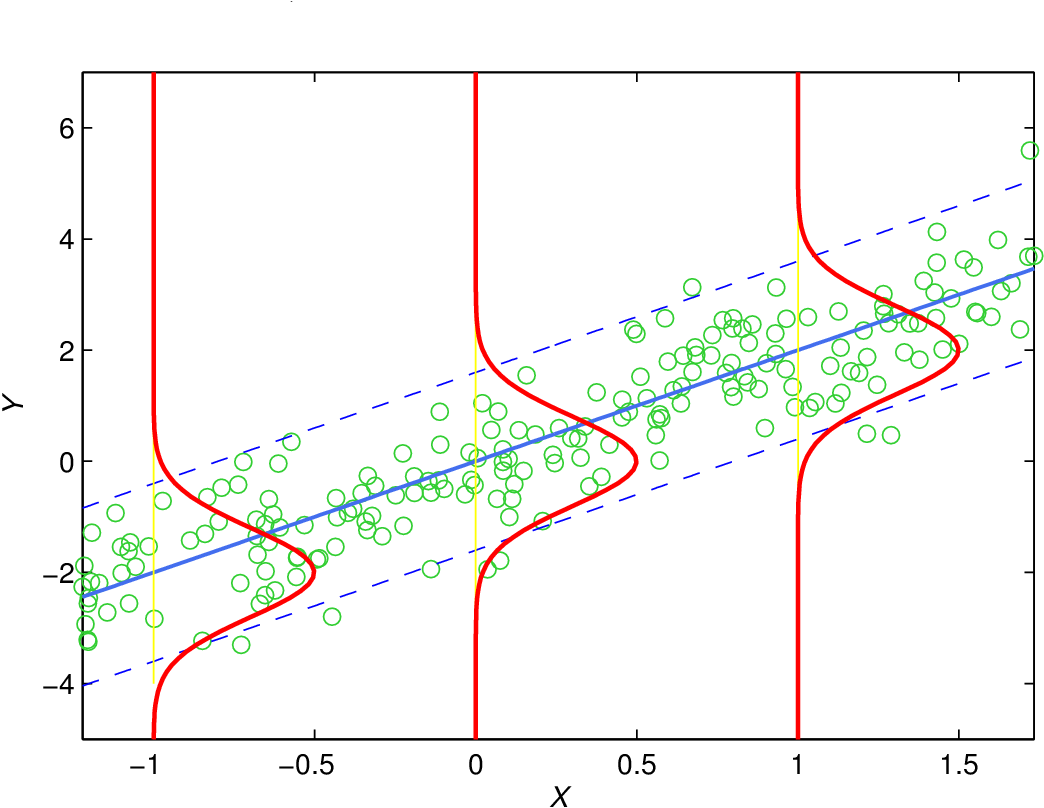
Příklad 3.2. Regresní přímka v klasickém lineárním regresním modelu:

jsou pro nezávislé náhodné veličiny,

je identická linkovací funkce, a jsou neznámé parametry  (přičemž je rušivým parametrem) a jsou známé kovariáty.

Obr. 1. Ukázka klasického regresního modelu s homogenním rozptylem.

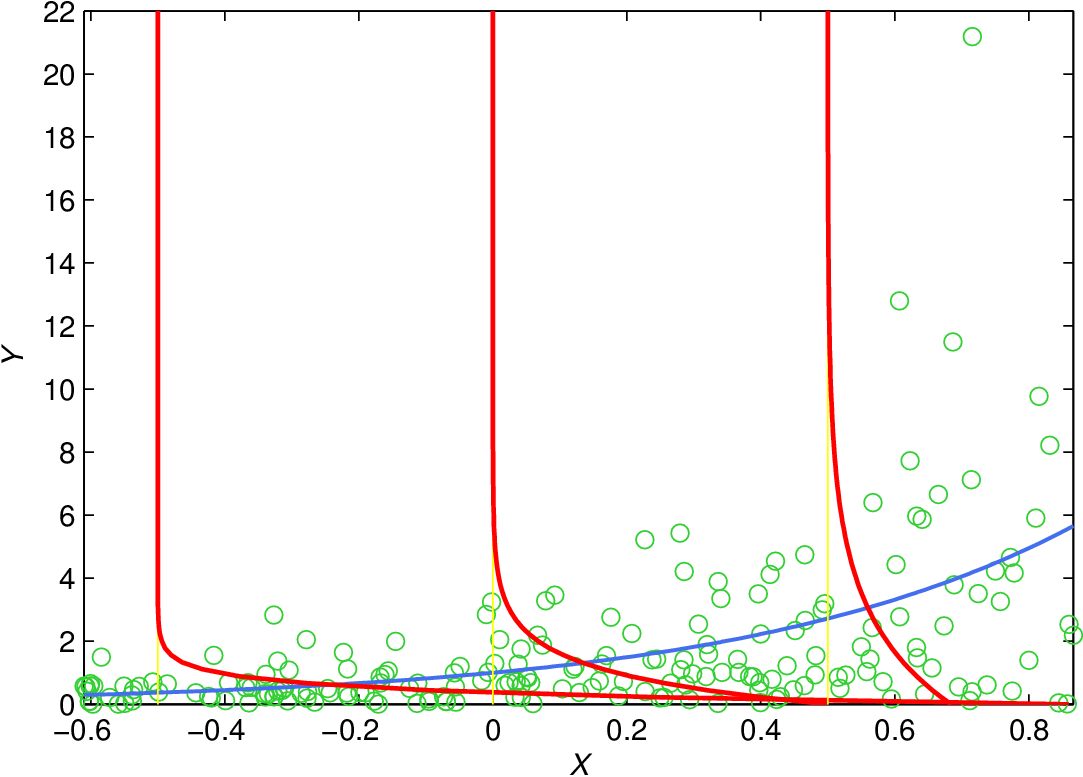
Příklad 3.3. (Regresní modely s logaritmickou linkovací funkcí pro exponenciálně a gamma rozdělené závisle proměnné):

jsou pro  nezávislé náhodné veličiny 

je logaritmická linkovací funkce,    jsou neznámé parametry a jsou známé kovariáty.

Obr. 2. Ukázka GLM modelu s linkovací funkcí pro exponenciálně rozdělenou náhodnou veličinu .

Jestliže jsou pro  nezávislé náhodné veličiny je logaritmická linkovací funkce,  a   jsou neznámé parametry ( je rušivý parametr) a jsou známé kovariáty.

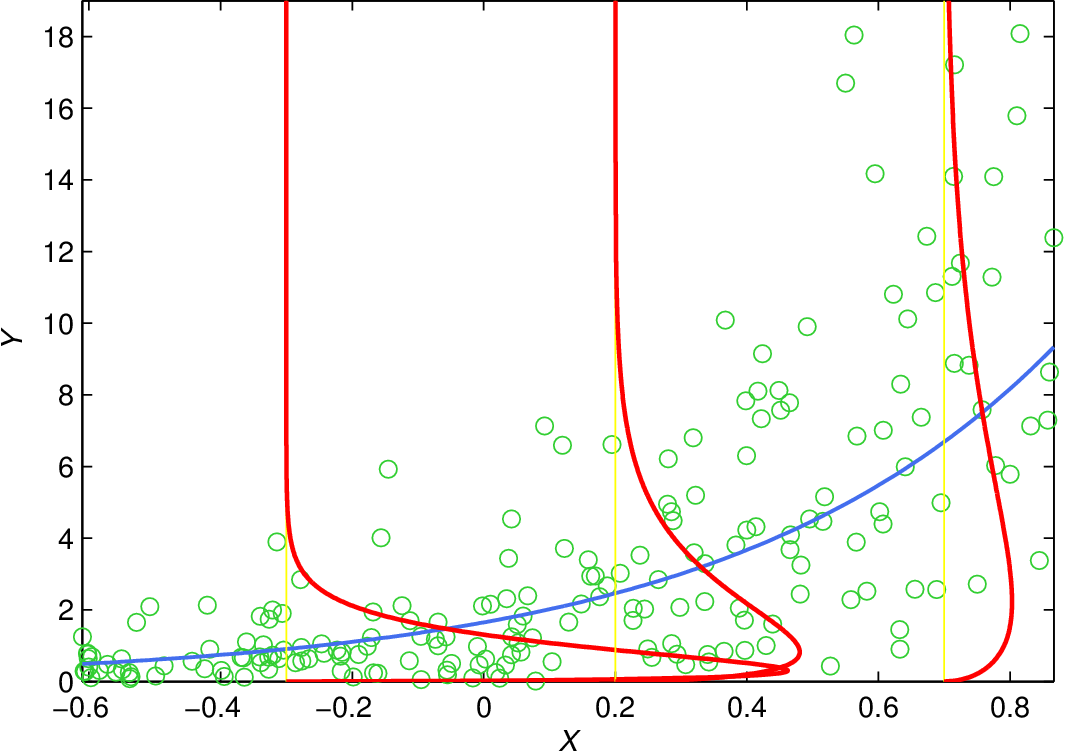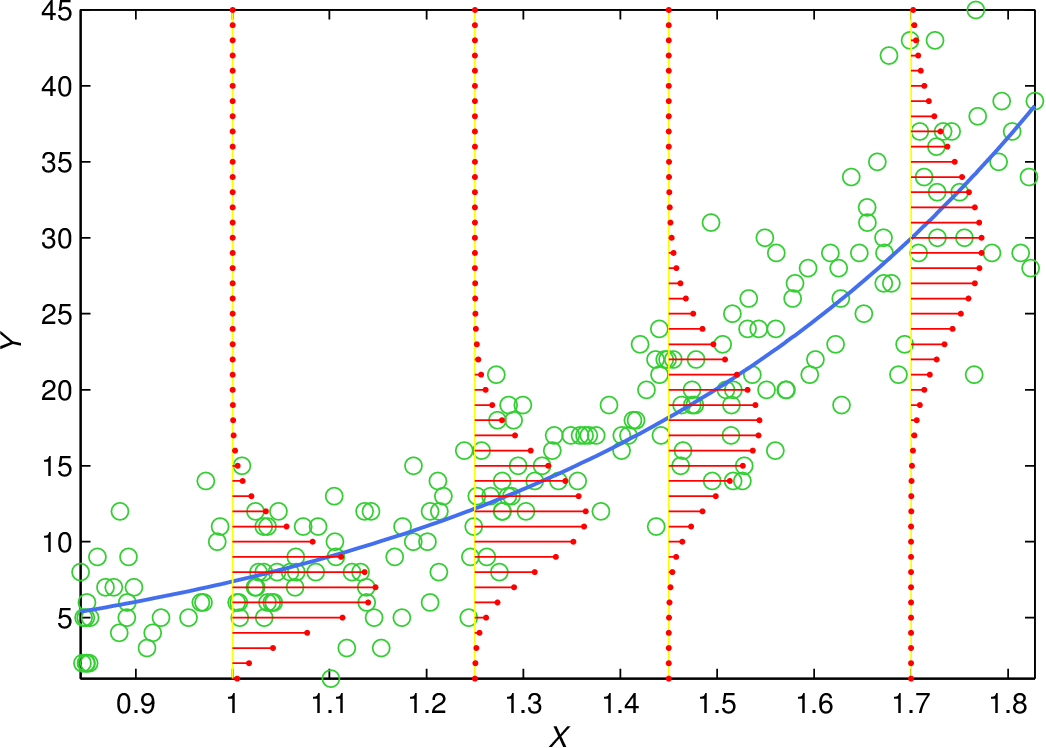
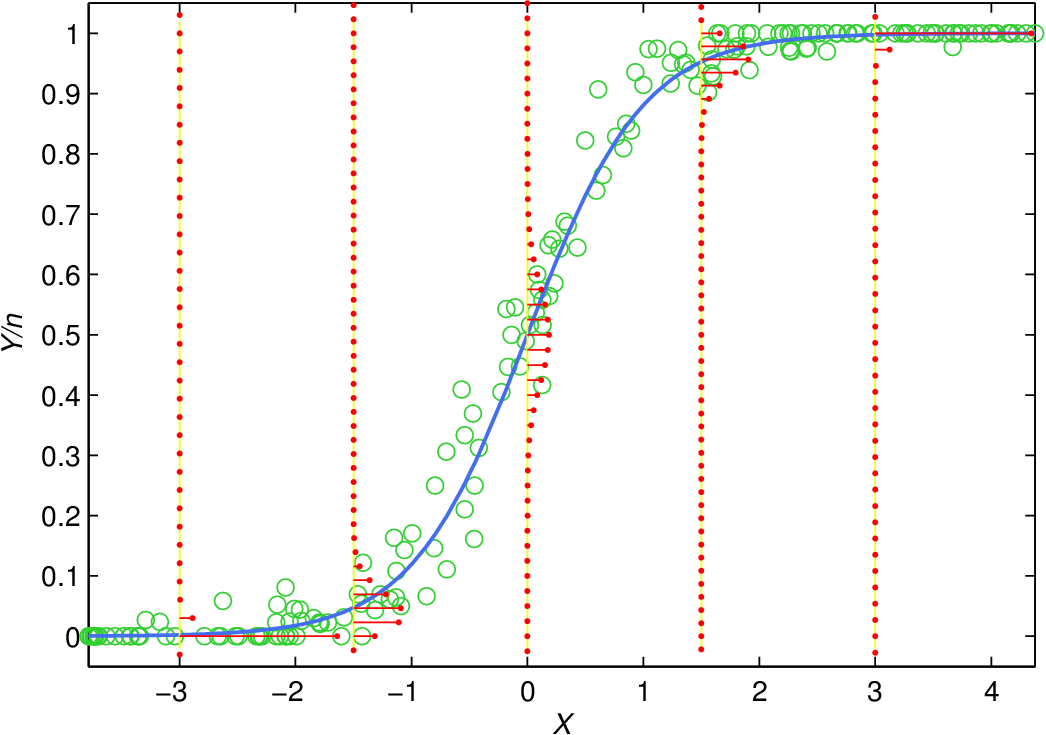
Obr. 3. Ukázka GLM modelu s linkovací funkcí  pro náhodnou veličinu s gamma rozdělením.

Příklad 3.4. Poissonovská regrese:

jsou pro  nezávislé náhodné veličiny

je logaritmická linkovací funkce,  jsou neznámé parametry a jsou známé kovariáty.

Obr. 4. Ukázka poissonovské regrese s linkovací funkcí

Příklad 3.5. Binomická regrese:

jsou pro  nezávislé náhodné veličiny, kde

je logistická linkovací funkce,  jsou neznámé parametry a jsou známé kovariáty.

Například ve farmaceutickém experimentu může být počet pacientů, kterým byla podána dávka nového léku a počet pacientů dávající pozitivní odpověď na danou dávku nového léku.

Jestliže pozorujeme, že roste spolu s  hledáme model, ve kterém je funkcí hodnot Proto model není vhodný, avšak obvykle pracuje dobře.

Obr. 5. Ukázka binomické regrese s linkovací funkcí

Příklad 3.6. Kontingenční tabulky:

jsou pro   nezávislé náhodné veličiny, například počet lidí -té etnické skupiny, kteří volí politickou stranu

Snahou bude testovat hypotézu

pro všechna kde jsou neznámé parametry, a tj. chceme testovat hypotézu, že volba strany a etnická příslušnost jsou nezávislé.

Připomeňme, že
takže
a za platnosti hypotézy
ekvivalentně	pro nějaké