Testy o parametrech normálního rozdělení, testy založené na centrální limitní větě

Pomocí intervalových (dolních, horních) odhadů, které jsme již dříve odvodili v části Bodové a intervalové odhady parametrů normálního rozdělení, dostáváme celou řadu kritických oblastí testů o parametrech normálního rozdělení. Poznamenejme, že se shodují s testy podílem věrohodností.

Přehled takto získaných testů pro JEDEN NÁHODNÝ VÝBĚR   podáváme v následující tabulce:

		Hypotézu zamítáme, pokud , tj.	Předoklady
			známé
			známé
			známé
			neznámé
			neznámé
			neznámé
			neznámé
			neznámé
			neznámé

V případě DVOU NEZÁVISLÝCH VÝBĚRŮ

•  první náhodný výběr  s výběrovým průměrem  a výběrový rozptylem ,
• druhý náhodný výběr  s výběrovým průměrem   a výběrový rozptylem ,
• a pokud označíme

pak následující tabulka se týká testů rovnosti středních hodnot a rozptylů:

		Hypotézu zamítáme, pokud , tj.	Předpoklady
			známé
			neznámé
			neznámé

Následující tabulka nabízí ASYMPTOTICKÉ TESTY pro náhodné výběry  s konečnými druhými momenty (s výběrovým průměrem  a se _, což je (slabě) konzistentní odhad rozptylu ):  

		Hypotézu  zamítáme, pokud	Předpoklady

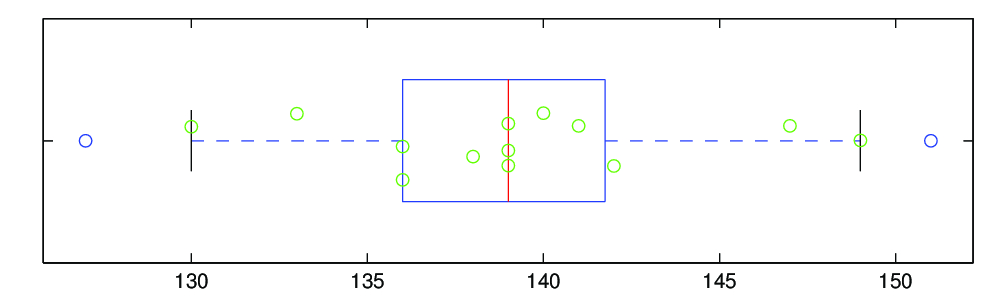
Příklad 7.2. (VÝŠKA DESETILETÝCH CHLAPCŮ) V roce 1961 byla u 15 náhodně vybraných chlapců z populace všech desetiletých chlapců žijících v Československu zjištěna výška

Výšky 15 desetiletých chlapců

Je známo, že každá následující generace je v průměru o něco vyšší než generace předcházející. Můžeme se tedy ptát, zda průměr  zjištěný v náhodném výběru rozsahu  znamená, že na hladině máme zamítnout nulovou hypotézu  (zjištění z roku 1951) ve prospěch alternativní hypotézy .

Rozptyl , zjištěný v roce 1951 (kdy se provádělo rozsáhlé šetření), můžeme považovat za známý, neboť variabilita výšek zůstává (na rozdíl od střední výšky) téměř nezměněná.
 

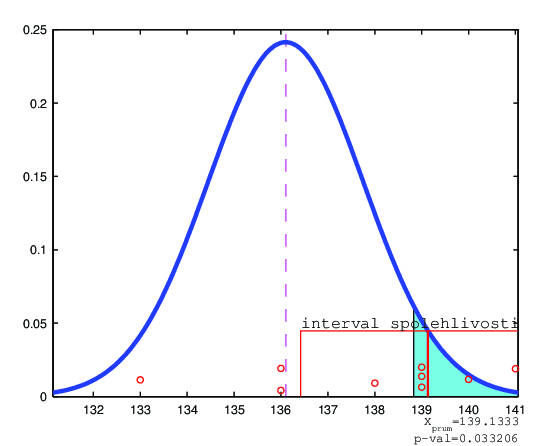
Řešení. (I) TESTOVÁNÍ NULOVÉHYPOTÉZY POMOCÍ PIVOTOVÉ STATISTIKY  A KRITICKÉ HODNOTY.

Protože kritický obor lze ekvivalentně vyjádřit i takto

počítejme    Protože  překračuje kritickou hodnotu (získáme pomocí R, a to příkazem  „rnorm(0.95)“) nulovou hypotézu na hladině zamítneme ve prospěch alternativní hypotézy, že se střední výška desetiletých hochů zvětšila. 

(II) TESTOVÁNÍ NULOVÉ HYPOTÉZY POMOCÍ p-HODNOTY

Dosažená hladina odpovídající testové statistice (tj. tzv. p-hodnota, anglicky P-value, significance value), což je nejmenší hladina testu, při které bychom ještě hypotézu  zamítli, je rovna 0.033 (opět získáme pomocí R příkazem   „1 - pnorm(mean(x),mean=136.1,sd=6.4/sqrt(n))“),   takže například při  by již dosažený výsledek nebyl statisticky významný.     Protože -hodnota je menší než zvolená hladina významnosti , hypotézu zamítáme.

(III) TESTOVÁNÍ NULOVÉ HYPOTÉZY POMOCÍ INTERVALU SPOLEHLIVOSTI

Protože jde o jednostranný test, použijeme dolní odhad střední hodnoty 

Protože interval spolehlivosti  nepokrývá hodnotu , proto nulovou hypotézu na na hladině významnosti  zamítáme.

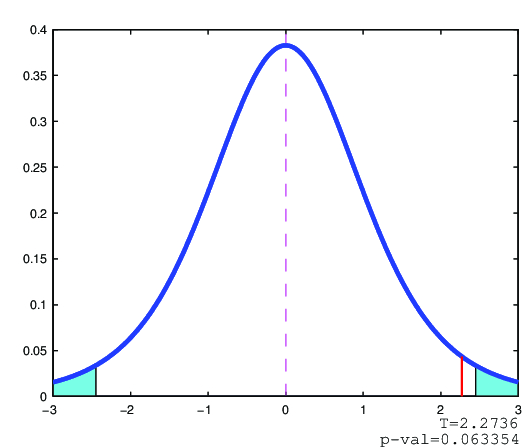
Příklad 7.3. PÁROVÝ TEST

Na sedmi rostlinách byl posuzován vliv fungicidního přípravku podle počtu skvrn na listech před a týden po použití přípravku. Otestujte, zdali má přípravek vliv na počet skvrn na listech. Data udávající počet skvrn na listech před a po použití přípravku: Počet skvrn na listech

 

Řešení. Za předpokladu, že náhodný výběr pochází z normálního rozdělení, tj.

  

 

pak

a statistika

má za platnosti nulové hypotézy   Studentovo rozdělení o  stupních volnosti.

(I) TESTOVÁNÍ NULOVÉ HYPOTÉZY POMOCÍ STATISTIKY T A INTERVALU SPOLEHLIVOSTI

Protože interval spolehlivosti pokrývá hodnotu na dané hladině významnosti hypotézu nemůžeme zamítnout.

(II) TESTOVÁNÍ NULOVÉ HYPOTÉZY POMOCÍ STATISTIKY T A KRITICKÉ HODNOTY

Vypočítáme-li hodnotu statistiky      a porovnáme s kvantilem Studentova rozdělení, tj.     takže hypotézu      nezamítáme.

 

(III) TESTOVÁNÍ NULOVÉ HYPOTÉZY POMOCÍ p-HODNOTY

Vypočítáme-li -hodnotu a porovnáme se zvolenou hladinou významnosti

takže hypotézu

nezamítáme.

Shrneme-li předchozí výsledky slovně, pak nulovou
hypotézu o tom, že

PŘÍPRAVEK NEMÁ VLIV NA POČET SKVRN

na hladině významnosti  nemůžeme zamítnout oproti alternativě o jeho vlivu.
 

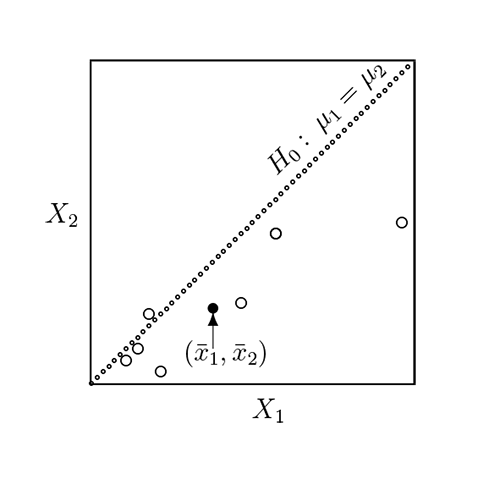
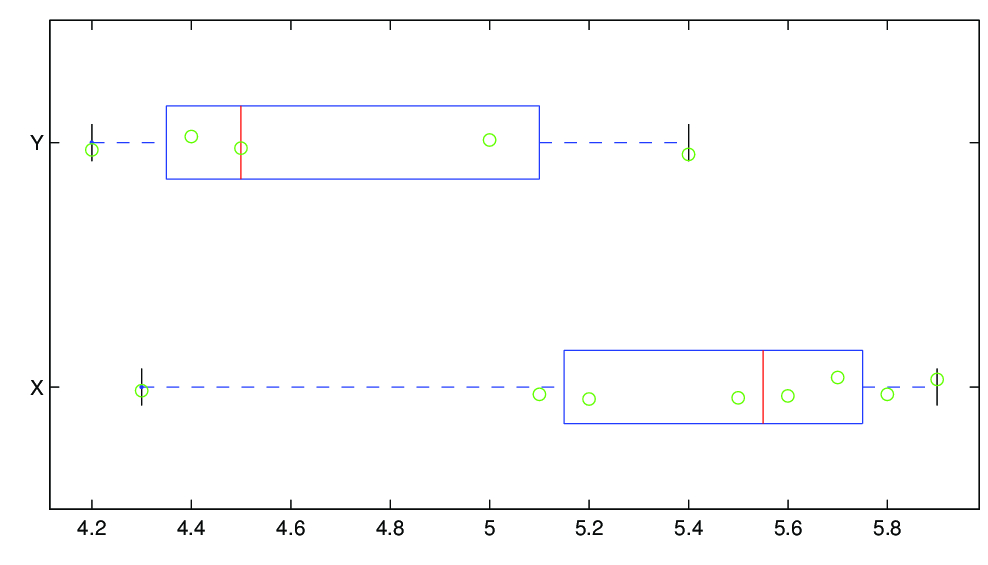
Příklad 7.4. (DVA NEZÁVISLÉ NÁHODNÉ VÝBĚRY Z NORMÁLNÍHO ROZDĚLENÍ PŘI NEZNÁMÝCH ALE STEJNÝCH ROZPTYLECH)  

Bylo vybráno 13 polí stejné kvality. Na 8 z nich se zkoušel nový způsob hnojení, zbývajících 5 bylo ošetřeno běžným způsobem. Výnosy pšenice uvedené v tunách na hektar jsou označeny u nového a u běžného způsobu hnojení. (převzato z knihy [2], str. 82, př. 8.2). Je třeba zjistit, zda způsob hnojení má vliv na výnos pšenice.

	Nechť  je náhodný výběr rozsahu  z normálního rozdělení   je jeho výběrový průměr a  jeho výběrový rozptyl.    Dále nechť  je náhodný výběr rozsahu  z normálního rozdělení ,   je jeho výběrový průměr a  jeho výběrový rozptyl.   Předpokládejme, že oba výběry jsou stochasticky nezávislé, tj. .

 

Řešení. Chceme-li testovat hypotézu, že rozdíl středních hodnot je nulový (při neznámém rozptylu ), za pivotovou statistiku zvolíme statistiku

kde

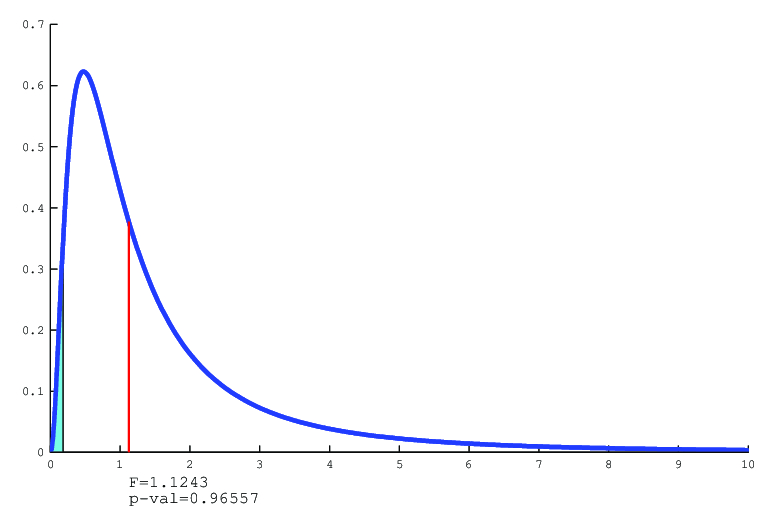
Chceme-li použít , měli bychom být přesvědčeni o tom, že rozptyly obou výběrů se významně neliší. Budeme tedy nejprve testovat hypotézu  

,

že podíl obou rozptylů je roven jedné proti alternativě, že se nerovná

za pivotovou statistiku zvolíme statistiku

 

(a)	Můžeme například vypočítat statistiku  za platnosti nulové hypotézy a porovnat ji s příslušnými oboustrannými kvantily.
	Protože     vidíme, že není ani větší než horní kritický bod, ani menší než dolní kritický bod, takže hypotézu o rovnosti rozptylů proti alternativě nerovnosti nezamítáme a můžeme konstatovat, že data nejsou v rozporu s testovanou hypotézou.
(b)	Další možností je spočítat dosaženou hladinu významnosti, tj. -hodnotu (pomocí R: 2*min(1-pf(var(x)/var(y),n1-1,n2-1), pf(var(x)/var(y),n1-1,n2-1)) a srovnat se zvolenou hladinou testu : Protože -hodnota je výrazně větší než zvolená hladina testu, hypotézu o rovnosti rozptylů proti alternativě nerovnosti nezamítáme. Můžeme také říci, že data nejsou v rozporu s testovanou hypotézou.
(c)	A naposledy můžeme ještě zkonstruovat  interval spolehlivosti pro podíl rozptylů  a zjistit, zda pokrývá hodnotu . Protože dostáváme interval , který pokrývá jedničku, hypotézu nezamítáme.

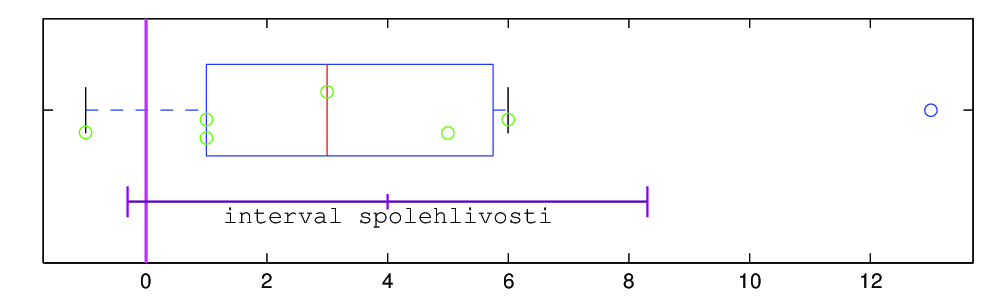
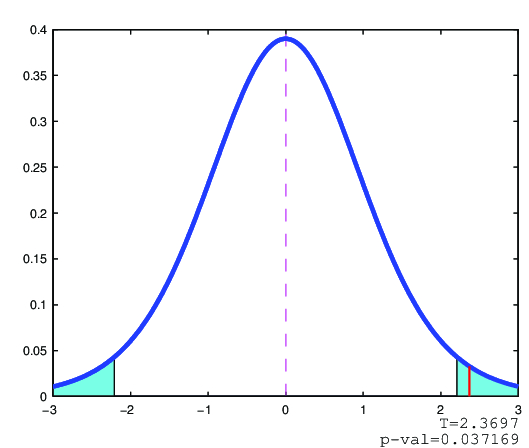
Díky předchozímu zjištění již můžeme bez obav testovat hypotézu  proti alternativě  a provedeme to opět třemi způsoby:

(I) TESTOVÁNÍ NULOVÉ HYPOTÉZY POMOCÍ INTERVALU SPOLEHLIVOSTI

 

Protože interval spolehlivosti nepokrývá nulu, na dané hladině významnosti hypotézu zamítáme ve prospěch alternativy.

(II) TESTOVÁNÍ NULOVÉ HYPOTÉZY POMOCÍ STATISTIKY T A KRITICKÉ HODNOTY

Vypočítáme-li hodnotu statistiky      a porovnáme s kvantilem Studentova rozdělení, tj.     takže hypotézu     zamítáme.

(III) TESTOVÁNÍ NULOVÉ HYPOTÉZY POMOCÍ p-HODNOTY

Vypočítáme-li -hodnotu a porovnáme se zvolenou hladinou významnosti 

takže hypotézu

zamítáme.

Shrneme-li předchozí výsledky slovně, pak nulovou hypotézu o tom, že

HNOJENÍ JE STEJNĚ ÚČINNÉ

na hladině významnosti  zamítáme ve prospěch alternativy, že má rozdílné účinky.